1707: [Usaco2007 Nov]tanning分配防晒霜
Time Limit: 5 Sec Memory Limit: 64 MBSubmit: 810 Solved: 387
[Submit][Status][Discuss]
Description
奶牛们计划着去海滩上享受日光浴。为了避免皮肤被阳光灼伤,所有C(1 <= C <= 2500)头奶牛必须在出门之前在身上抹防晒霜。第i头奶牛适合的最小和最 大的SPF值分别为minSPF_i和maxSPF_i(1 <= minSPF_i <= 1,000; minSPF_i <= maxSPF_i <= 1,000)。如果某头奶牛涂的防晒霜的SPF值过小,那么阳光仍然能 把她的皮肤灼伤;如果防晒霜的SPF值过大,则会使日光浴与躺在屋里睡觉变得 几乎没有差别。为此,奶牛们准备了一大篮子防晒霜,一共L(1 <= L <= 2500)瓶。第i瓶 防晒霜的SPF值为SPF_i(1 <= SPF_i <= 1,000)。瓶子的大小也不一定相同,第i 瓶防晒霜可供cover_i头奶牛使用。当然,每头奶牛只能涂某一个瓶子里的防晒霜 ,而不能把若干个瓶里的混合着用。 请你计算一下,如果使用奶牛们准备的防晒霜,最多有多少奶牛能在不被灼 伤的前提下,享受到日光浴的效果?
Input
* 第1行: 2个用空格隔开的整数:C和L
* 第2..C+1行: 第i+1行给出了适合第i头奶牛的SPF值的范围:minSPF_i以及 maxSPF_i * 第C+2..C+L+1行: 第i+C+1行为了第i瓶防晒霜的参数:SPF_i和cover_i,两个 数间用空格隔开。
Output
* 第1行: 输出1个整数,表示最多有多少头奶牛能享受到日光浴
Sample Input
3 2
3 10
2 5
1 5
6 2
4 1
输入说明:
一共有3头奶牛,2瓶防晒霜。3头奶牛适应的SPF值分别为3..10,2..5,以
及1..5。2瓶防晒霜的SPF值分别为6(可使用2次)和4(可使用1次)。可能的分
配方案为:奶牛1使用第1瓶防晒霜,奶牛2或奶牛3使用第2瓶防晒霜。显然,最
多只有2头奶牛的需求能被满足。
3 10
2 5
1 5
6 2
4 1
输入说明:
一共有3头奶牛,2瓶防晒霜。3头奶牛适应的SPF值分别为3..10,2..5,以
及1..5。2瓶防晒霜的SPF值分别为6(可使用2次)和4(可使用1次)。可能的分
配方案为:奶牛1使用第1瓶防晒霜,奶牛2或奶牛3使用第2瓶防晒霜。显然,最
多只有2头奶牛的需求能被满足。
Sample Output
2
题目大意:有c只奶牛,有一个涂抹防晒霜的上限和下限。然后有l瓶放晒霜,每瓶能给w头奶牛涂。
奶牛晒日光浴的条件是涂的防晒霜在范围之内。求最多有多少头奶牛能晒日光浴。
题解:贪心
对于第i瓶放晒霜,找出所有涂抹它能满足条件的奶牛。先满足上限低的。
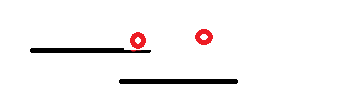
假设有两头奶牛,黑线表示区间,红圈表示防晒霜的spf。对于从左边数第一个红圈,两头奶牛都能满足。但是,要把这个
防晒霜给上限低的也就是右端更小的第一头奶牛。这样分配,两头奶牛都能晒日光浴,否则只有第二头。
所以按spf从小到大枚举,将牛的右端点从小到大排序并枚举看看是否符合要求。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxn 2550 using namespace std; int c,l,ans; struct COW{ int l,r; }cow[maxn]; struct FSS{ int spf,w; }fss[maxn]; bool cmp1(COW a,COW b){return a.r<b.r;} bool cmp2(FSS a,FSS b){return a.spf<b.spf;} int main(){ scanf("%d%d",&c,&l); for(int i=1;i<=c;i++)scanf("%d%d",&cow[i].l,&cow[i].r); for(int i=1;i<=l;i++)scanf("%d%d",&fss[i].spf,&fss[i].w); sort(cow+1,cow+c+1,cmp1);sort(fss+1,fss+l+1,cmp2); for(int i=1;i<=c;i++) for(int j=1;j<=l;j++) if(fss[j].w&&cow[i].l<=fss[j].spf&&fss[j].spf<=cow[i].r){ ans++;fss[j].w--;break; } printf("%d ",ans); return 0; }