求全排列和组合问题

1.排列：全排列n!
　　使用next_permutation函数

输出序列{1,2,3,4}字典序的全排列。
#include <iostream>
#include<algorithm>
using namespace std;

int main(int argc, char** argv) {
int a[4]={1,2,3,4};
sort(a,a+4);
do{
//cout<<a[0]<<" "<<a[1]<<" "<<a[2]<<" "<<a[3]<<endl;
for(int i=0;i<4;i++)
cout<<a[i]<<" ";
cout<<endl;
}while(next_permutation(a,a+4));
return 0;
}

输入任意一个字符串，输出其字典序的全排列

#include <iostream>
#include<algorithm>
using namespace std;

int main(int argc, char** argv) {
string str;
cin>>str;
sort(str.begin(),str.end());
do{
cout<<str<<endl;
}while(next_permutation(str.begin(),str.end()));
return 0;
}

递归法

设一组数p = {r1, r2, r3, … ,rn}, 全排列为perm(p)，pn = p – {rn}。则perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), … , rnperm(pn)。当n = 1时perm(p} = r1。
如：求{1, 2, 3, 4, 5}的全排列
1、首先看最后两个数4, 5。 它们的全排列为4 5和5 4, 即以4开头的5的全排列和以5开头的4的全排列。
由于一个数的全排列就是其本身，从而得到以上结果。
2、再看后三个数3, 4, 5。它们的全排列为3 4 5、3 5 4、 4 3 5、 4 5 3、 5 3 4、 5 4 3 六组数。
即以3开头的和4,5的全排列的组合、以4开头的和3,5的全排列的组合和以5开头的和3,4的全排列的组合.

#include <
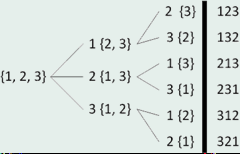
iostream>
using namespace std;

void Perm(int start, int end, int a[]) {
//得到全排列的一种情况，输出结果
if (start == end) {
for (int i = 0; i < end; i++)
cout << a[i] << ' ';
cout << endl;
return;
}
for (int i = start; i < end; i++) {
swap(a[start], a[i]); //交换
Perm(start + 1, end, a); //分解为子问题a[start+1,...,end-1]的全排列
swap(a[i], a[start]); //回溯
}
}
int main() {
int i, n, a[10];
while (cin >> n, n) {
for (i = 0; i < n; i++)
{
a[i] = i + 1;
}
Perm(0, n, a);
}
return 0;
}

2.组合：C(n,k)，n个数中任取k个数
递归法

实际上就是在n个数中，标记k个数，然后输出这k个数的过程。使用一个visited数组来记录相应下标的数是否被选中。

#include <iostream>
using namespace std;

void dfs(int pos, int cnt, int n, int k, int a[],bool visited[]) {
//已标记了k个数，输出结果
if (cnt == k) {
for (int i = 0; i < n; i++)
if (visited[i]) cout << a[i] << ' ';
cout << endl;
return;
}

//处理到最后一个数，直接返回
if (pos == n) return;

//如果a[pos]没有被选中
if (!visited[pos]) {
//选中a[pos]
visited[pos] = true;
//处理在子串a[pos+1, n-1]中取出k-1个数的子问题
dfs(pos + 1, cnt + 1, n, k, a,visited);
//回溯
visited[pos] = false; 
}
//处理在子串a[pos+1, n-1]中取出k个数的问题
dfs(pos + 1, cnt, n, k, a, visited);
}
int main() {
int i, n, k;
while (cin >> n >> k, n || k) 
{
int *a = new int[n];
bool *visited = new bool[n];
for (i = 0; i < n; i++)
{
a[i] = i + 1;
visited[i] = false;
}
dfs(0, 0, n, k, a, visited);
delete[] a;
delete[] visited;
}
getchar();
return 0;
}

‘01’转换法

本程序的思路是开一个数组，其下标表示1到n个数，数组元素的值为1表示其代表的数被选中，为0则没选中。
首先初始化，将数组前n个元素置1，表示第一个组合为前n个数。
然后从左到右扫描数组元素值的“10”组合，找到第一个“10”组合后将其变为“01”组合，同时将其左边的所有“1”全部移动到数组的最左端。
当第一个“1”移动到数组的n-m的位置，即n个“1”全部移动到最右端时，就得到了最后一个组合。
例如求5中选3的组合：
1 1 1 0 0 //1,2,3

1 1 0 1 0 //1,2,4

1 0 1 1 0 //1,3,4

0 1 1 1 0 //2,3,4

1 1 0 0 1 //1,2,5

1 0 1 0 1 //1,3,5

0 1 1 0 1 //2,3,5

1 0 0 1 1 //1,4,5

0 1 0 1 1 //2,4,5

0 0 1 1 1 //3,4,5

#include <iostream>
using namespace std;

//输出结果
void printRes(int* a, bool* index, int n)
{
for (int i=0;i<n;i++)
{
if (index[i])
{
cout << a[i] << " ";
}
}
cout << endl;
}

//检查最后k个位置是否已全变成0
bool hasDone(bool* index, int n, int k)
{
for (int i=n-1;i>=n-k;i--)
{
if (!index[i])
{
return false;
}
}
return true;
}

void Comb(int* a, int n, int k)
{
bool *index = new bool[n]();
//选中前k个位置
for (int i = 0; i < k; i++)
{
index[i] = true;
}
printRes(a, index, n);

while (!hasDone(index, n, k))
{
//从左到右扫描数组
for (int i = 0; i < n - 1; i++)
{
//找到第一个“10”组合将其变成"01"组合
if (index[i] && !index[i + 1])
{
index[i] = false;
index[i + 1] = true;

//将"01"组合左边的1移到最左边
int count = 0;
for (int j = 0; j < i; j++)
{
if (index[j])
{
index[j] = false;
index[count++] = true;
}
}
printRes(a, index, n);
break;
}
}
}
delete[] index;
}
int main()
{
int n,k;
while (cin>>n>>k)
{
int *a = new int[n]();
for (int i = 0; i < n; i++)
{
a[i] = i+1;
}
Comb(a, n, k);
delete[] a;
}

return 0;
}