本文地址:http://www.cnblogs.com/zzw-in/p/Bilinear_interpolation.html
首先我们来看一下双线性插值的定义:
百度百科上的定义:双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
根据定义,双线性插值就是分别在两个不同方向进行线性插值,这里的"两个方向"一般对应着xy轴。
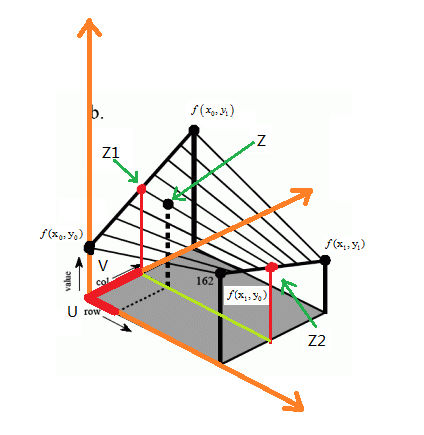
如下图所示:
那么如果先对y方向进行插值再对x轴方向进行插值的话,计算思路如下:
同理,如果先对y方向进行插值再对x轴方向进行插值的话,计算思路如下:
上面就是双线性插值的计算思路。
好的,现在已经对双线性插值的概念有了比较清楚的认识,那么接下来就看看双线新插值在图像缩放里面的应用吧。
在图像缩放中,如果源图像是的图像,而缩放后的图像为,那么原图与缩放后的图在xy方向上的缩放比为![]()
由于在原图当中并不存在点P的像素值,为了求得这个对应于缩放后的图像在(i,j)位置的像素值,我们就需要根据该位置周围的4个像素点的像素值进行双线性插值得到该点的像素值,这样我们就可以求得缩放后的图像在位置(i,j)上的像素值了。对缩放后的图像的每个像素点遍历一遍,就可以得到整幅缩放后的图像了。整个思路就是:
根据上面的双线性插值的公式:
所以,经整理可得:
在这里,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数。
理论上面已经讲得差不多了,下面来看一下C#的实现代码:
double xRatio = (double)rect.Width / newRect.Width;//横向比 double yRatio = (double)rect.Height / newRect.Height;//纵向比 unsafe { //源图像的扫描起点 byte* ptr1 = (byte*)(bmpData1.Scan0); //新图像的扫描起点 byte* ptr2 = (byte*)(bmpData2.Scan0); //对新图像的像素点进行遍历 for (int i = 0; i < bmpData2.Height; i++) { double srcY = i * yRatio;//源图像“虚”坐标的y值 int IntY = (int)srcY;//向下取整 double v = srcY - IntY;//获取小数部分 double v1 = 1.0 - v; for (int j = 0; j < bmpData2.Width; j++) { double srcX = j * xRatio;//源图像“虚”坐标的x值 int IntX = (int)srcX;//向下取整 double u = srcX - IntX;//获取小数部分 double u1 = 1.0 - u; int Index00 = IntY * stride1 + IntX * 3;//得到原图左上角的像素位置 int Index10; //原图左下角的像素位置 if (IntY < bmpData1.Height - 1) { Index10 = Index00 + stride1; } else { Index10 = Index00; } int Index01; //原图右上角的像素位置 int Index11; //原图右下角的像素位置 if (IntX < bmpData1.Width - 1) { Index01 = Index00 + 3; Index11 = Index10 + 3; } else { Index01 = Index00; Index11 = Index10; } double temp0 = (v1 * (u * ptr1[Index01] + u1 * ptr1[Index00]) + v * (u * ptr1[Index11] + u1 * ptr1[Index10])); double temp1 = (v1 * (u * ptr1[Index01 + 1] + u1 * ptr1[Index00 + 1]) + v * (u * ptr1[Index11 + 1] + u1 * ptr1[Index10 + 1])); double temp2 = (v1 * (u * ptr1[Index01 + 2] + u1 * ptr1[Index00 + 2]) + v * (u * ptr1[Index11 + 2] + u1 * ptr1[Index10 + 2])); ptr2[0] = (byte)temp0; ptr2[1] = (byte)temp1; ptr2[2] = (byte)temp2; ptr2 += 3; } ptr2 += offset2; } }
参考文章:
http://blog.sina.com.cn/s/blog_afe2af380101cadz.html
http://blog.csdn.net/qiqi5521/article/details/2207562
http://www.cnblogs.com/Imageshop/archive/2011/11/12/2246808.html#2922372
![clip_image001[23] clip_image001[23]](http://images0.cnblogs.com/blog/529617/201404/222246205453939.png)
![clip_image001[25] clip_image001[25]](http://images0.cnblogs.com/blog/529617/201404/222246212798080.png)
![clip_image001[33] clip_image001[33]](http://images0.cnblogs.com/blog/529617/201404/222246226853850.png)


![clip_image001[35] clip_image001[35]](http://images0.cnblogs.com/blog/529617/201404/222246260768748.png)
![clip_image001[39] clip_image001[39]](http://images0.cnblogs.com/blog/529617/201404/222246274512762.png)

