F. Geometrical Progression

http://codeforces.com/problemset/problem/758/F

F. Geometrical Progression

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

For given n, l and r find the number of distinct geometrical progression, each of which contains n distinct integers not less than l and not greater than r. In other words, for each progression the following must hold: l ≤ a_i ≤ r and a_i ≠ a_j , where a₁, a₂, ..., a_n is the geometrical progression, 1 ≤ i, j ≤ n and i ≠ j.

Geometrical progression is a sequence of numbers a₁, a₂, ..., a_n where each term after first is found by multiplying the previous one by a fixed non-zero number d called the common ratio. Note that in our task d may be non-integer. For example in progression 4, 6, 9, common ratio is .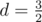

Two progressions a₁, a₂, ..., a_n and b₁, b₂, ..., b_n are considered different, if there is such i (1 ≤ i ≤ n) that a_i ≠ b_i.

Input

The first and the only line cotains three integers n, l and r (1 ≤ n ≤ 10⁷, 1 ≤ l ≤ r ≤ 10⁷).

Output

Print the integer K — is the answer to the problem.

Examples

Input

1 1 10

Output

10

Input

2 6 9

Output

12

Input

3 1 10

Output

8

Input

3 3 10

Output

2

Note

These are possible progressions for the first test of examples:

• 1;
• 2;
• 3;
• 4;
• 5;
• 6;
• 7;
• 8;
• 9;
• 10.

These are possible progressions for the second test of examples:

• 6, 7;
• 6, 8;
• 6, 9;
• 7, 6;
• 7, 8;
• 7, 9;
• 8, 6;
• 8, 7;
• 8, 9;
• 9, 6;
• 9, 7;
• 9, 8.

These are possible progressions for the third test of examples:

• 1, 2, 4;
• 1, 3, 9;
• 2, 4, 8;
• 4, 2, 1;
• 4, 6, 9;
• 8, 4, 2;
• 9, 3, 1;
• 9, 6, 4.
• 题意：在[l,r]区间中找项数为n的等比数列的不同个数;   

思路：首先讨论下 n = 1,2的情况，然后，找公比，应为r<=1e7,那么n不会超过23，当d为整数的时候那么d^(n-1)<=r;

从而选出d，然后当d为分数的时候，假设（a/b);那么我们只要枚举（a,b互质）的数，因为若不互质可化成互质，那么（a/b）^(n-1),假设第一个数为x，那么x要是b^(n-1)的

倍数，设x = k*(b)^(n-1);那么a，b必定是刚选出来的那些数中的数，不可能比选出来的数大，因为x = k*(b)^(n-1)<=r&&k*(b)^(n-1)<=n&&(k>=1);

那么枚举d来解k的范围;（l-1）< (a)^(n-1)*k&&k*(b^(n-1))<=r;

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL n,LL m){if(m == 0)return n;return gcd(m,n%m);}
LL ans[4000];
int main(void)
{
    LL n,l,r;LL ask = 0;
    scanf("%lld %lld %lld",&n,&l,&r);
    if(n == 1)
        printf("%lld
",r-l+1);
    else if(n == 2)
        printf("%lld
",(LL)(r-l+1)*(LL)(r-l));
    else if(n > 25)
        printf("0
");
    else
    {   int cn = 0;
        for(int i = 1;i <= 4000;i++)
        {   LL sum = 1;int j;
            for( j = 0;j < n-1;j++)
            {

                sum*=(LL)i; if(sum > r)break;
            }
            if(j == n-1)
            {
                ans[++cn] = sum;
            }
            else break;
        }
        for(int i = 1;i <= cn;i++)
        {
            for(int j = i+1;j <= cn;j++)
            {
                if(gcd(i,j) == 1)
                {
                    LL p = r/ans[j];
                    LL q = (l-1)/ans[i];
                    if(p >= q)
                        ask+=p-q;
                }
            }
        }
        printf("%lld
",ask*(LL)2);
    }
    return 0;
}