Harry Potter and the Hide Story
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2809 Accepted Submission(s): 715
Problem Description
iSea is tired of writing the story of Harry Potter, so, lucky you, solving the following problem is enough.
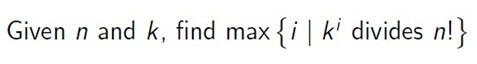
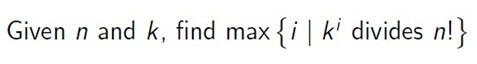
Input
The first line contains a single integer T, indicating the number of test cases.
Each test case contains two integers, N and K.
Technical Specification
1. 1 <= T <= 500
2. 1 <= K <= 1 000 000 000 000 00
3. 1 <= N <= 1 000 000 000 000 000 000
Each test case contains two integers, N and K.
Technical Specification
1. 1 <= T <= 500
2. 1 <= K <= 1 000 000 000 000 00
3. 1 <= N <= 1 000 000 000 000 000 000
Output
For
each test case, output the case number first, then the answer, if the
answer is bigger than 9 223 372 036 854 775 807, output “inf” (without
quote).
Sample Input
2
2 2
10 10
Sample Output
Case 1: 1
Case 2: 2
思路:素数分解;
当K = 1的时候肯定输出inf;我们将n分解成素数的乘积,那么我们需要找m!分解后含有这些素数的个数cnt[pi],那么最高次就是min(cnt[pi]/cnt1[pi]);cnt1[pi]为n中pi的个数。
1 #include<stdio.h> 2 #include<algorithm> 3 #include<iostream> 4 #include<queue> 5 #include<set> 6 #include<math.h> 7 #include<string.h> 8 using namespace std; 9 typedef unsigned long long LL; 10 bool prime[10000015]; 11 LL ans[1000000]; 12 LL prime_table[10000]; 13 LL pr_cnt[10000]; 14 LL pr_cn[10000]; 15 LL slove(LL n,LL m,int cn); 16 int main(void) 17 { 18 int T; 19 scanf("%d",&T); 20 int i,j; 21 for(i = 2; i < 10000; i++) 22 { 23 if(!prime[i]) 24 { 25 for(j = i; (i*j) <= 10000010; j++) 26 { 27 prime[i*j] = true; 28 } 29 } 30 } 31 int cn = 0; 32 for(i = 2; i < 10000010; i++) 33 if(!prime[i])ans[cn++] = i; 34 int __ca = 0; 35 while(T--) 36 { 37 LL n,m; 38 __ca++; 39 scanf("%llu %llu",&m,&n); 40 printf("Case %d: ",__ca); 41 if(n == 1) 42 printf("inf "); 43 else 44 { 45 printf("%llu ",slove(n,m,cn)); 46 } 47 } 48 return 0; 49 } 50 LL slove(LL n,LL m,int cn) 51 { 52 int bn = 0; 53 int f = 0; 54 bool flag = false ; 55 memset(pr_cnt,0,sizeof(pr_cnt)); 56 memset(pr_cn,0,sizeof(pr_cn)); 57 while(n>1) 58 { 59 while(n%ans[f]==0) 60 { 61 if(!flag) 62 { 63 flag = true; 64 bn++; 65 prime_table[bn] = ans[f]; 66 } 67 pr_cnt[bn]++; 68 n/=ans[f]; 69 } 70 f++; 71 flag = false; 72 if((LL)ans[f]*(LL)ans[f] > n) 73 break; 74 } 75 if(n > 1) 76 { 77 bn++; 78 prime_table[bn] = n; 79 pr_cnt[bn]++; 80 }//printf("%d ",n); 81 LL maxx = -1; 82 for(int i = 1; i <= bn; i++) 83 { //printf("%llu ",prime_table[i]); 84 LL v = m; 85 while(v) 86 { 87 v/=(LL)prime_table[i]; 88 pr_cn[i]+=v; 89 } 90 if(maxx == -1) 91 { 92 maxx = (LL)pr_cn[i]/(LL)pr_cnt[i]; 93 } 94 else 95 maxx = min((LL)pr_cn[i]/(LL)pr_cnt[i],maxx); 96 } 97 return maxx; 98 }