codeforce-424C. Magic Formulas(数学)

C. Magic Formulas

time limit per test:2 seconds     memory limit per test:256 megabytes

 

input

standard input

output

standard output

People in the Tomskaya region like magic formulas very much. You can see some of them below.

Imagine you are given a sequence of positive integer numbers p1, p2, ..., pn. Lets write down some magic formulas:

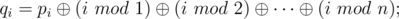
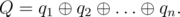
Here, "mod" means the operation of taking the residue after dividing.

The expression 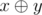 means applying the bitwise xor (excluding "OR") operation to integers x and y. The given operation exists in all modern programming languages. For example, in languages C++ and Java it is represented by "^", in Pascal — by "xor".

People in the Tomskaya region like magic formulas very much, but they don't like to calculate them! Therefore you are given the sequence p, calculate the value of Q.

Input

The first line of the input contains the only integer n (1 ≤ n ≤ 106). The next line contains n integers: p1, p2, ..., pn (0 ≤ pi ≤ 2·109).

Output

The only line of output should contain a single integer — the value of Q.

Sample test(s)

input

3
1 2 3

output

3

  

 为公式2.     

因为异或运算满足交换律和结合律，

所以公式 = p1^p2^……^pn^(1%1)^(1%2)^……(1%n)^(2%1)%(2%2)^……^(2%n)^……^(n%1)^(n%2)^……^(n%n)

 =p1^p2^……^pn^(1%1)^(2%1)^……(n%1)^(1%2)^(2%2)^……^(n%2)^……^(1%n)%(2%n)^……^(n%n).

公式2=(1%1)^(1%2)^……(1%n)^(2%1)%(2%2)^……^(2%n)^……^(n%1)^(n%2)^……^(n%n)

 =p1^p2^……^pn^(1%1)^(2%1)^……(n%1)^(1%2)^(2%2)^……^(n%2)^……^(1%n)%(2%n)^……^(n%n).

那么公式2再以后面模数分类结合。

可以的到模数从1-n的通项为S_k=(1%k)^(2%k)^.....(n%k).

那么k是从1-n取不同的数，然后公式2就为S₁^S_2.....^S_n。

关键是Sk的求解，每一个k，S_k=(1%k)^(2%k)^.....(n%k)，其中（n%k）的值只能取（0-k）,那没 （1，n）是连续的所以必定有周期，

由于a^a=0,a^0=a;

举个例子；假如n=9,k=4;

1	2	3	0
1	2	3	0
1

结果就是1，上边的两行a^a=0，所以只剩下1；

又如当n=25，k=7时。（1%7)、(2%7)……(25%7)的结果如下表。

1	2	3	4	5	6	0
1	2	3	4	5	6	0
1	2	3	4	5	6	0
1	2	3	4

上边的整行就是n/k;

下面剩下的就是n%k;

那么如果上面为偶数行&&(n%k)>=1的话那么最后的sk=1^...(n%k);

如果上面为偶数行&&n%k==0,那么sk=0;

如果上面为奇数行&&(n%k)==0，sk=1^...k;

如果上面为奇数行&&（n%k)>=1,那么sk=(n%k+1)^....k;

这样的话每个sk就很容易计算了。

#include<stdio.h>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#include<iostream>
#include<queue>
#include<math.h>
typedef long long ll;
ll a[1000005];
ll dd[1000005];
ll cc[1000005];
int main(void)
{
    ll i,j,k,p,q;
    ll pp=0;
    dd[0]=0;
    while(scanf("%I64d",&k)!=EOF)
    {
        cc[k+1]=0;
        for(i=1; i<=k; i++)
        {
            scanf("%I64d",&a[i]);
            pp^=a[i];
            dd[i]=(dd[i-1]^i);
        }
        for(i=k; i>=0; i--)
        {
            cc[i]=cc[i+1]^i;
        }
        /*那么如果上面为偶数行&&(n%k)>=1的话那么最后的sk=1^...(n%k);

        如果上面为偶数行&&n%k==0,那么sk=0;
        如果上面为奇数行&&(n%k)==0，sk=1^...k;

        如果上面为奇数行&&（n%k)>=1,那么sk=(n%k+1)^....k;*/
        for(i=1; i<=k; i++)
        {
            p=k/i;
            q=k%i;
            if(p%2==1)
            {
                pp^=(cc[i]^cc[q+1]);
            }
            else if(p%2==0)
            {
                pp^=dd[q];
            }
        }
        printf("%I64d
",pp);
    }
    return 0;
}