感觉又开了一个天坑真是开心...
还是先贴神犇链接补充阅读吧:
http://lazycal.logdown.com/posts/202331-bzoj3572
http://www.cnblogs.com/wuyuhan/p/5521249.html
例题 bzoj3572 世界树
给定一棵树,有若干个询问,每次给定m个点,每个点都被这m个点中最近(距离相同,编号小的近)的点管辖。问m个点分别管几个点。
n<=300000,q<=300000,∑m<=300000。
首先我们发现∑m是不大的,所以我们可以对于每一个询问点乱搞。
我们发现这类题目中我们可以把一些询问点单独搞出来组成一棵树,这样只有这些询问点是有用的。哦不对,还有一些询问点的lca?
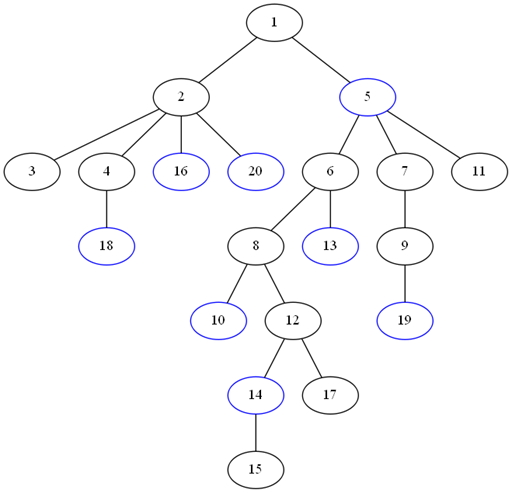
为了和谐,我们来直观地感受一下...比如这里我生成了一棵20个点的树。蓝色的是询问点。红色点就会在虚树上。
观察这些虚树上的点,我们发现我们似乎是需要把询问点按dfs序排序一下,然后把相邻点取个lca然后乱搞一下?
听起来好像很有道理,不过这™能写?
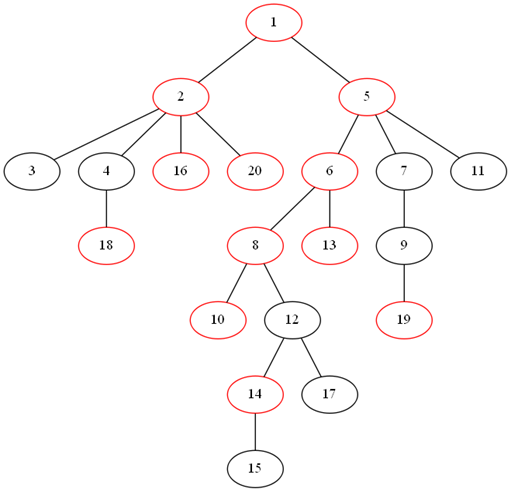
基于这样的想法,我们来考虑另外一种做法,我们用一个栈来维护虚树的“当前这一坨东西”...例如我们在栈中加入了18。然后接下来打算加入一个16。
我们现在发现这个栈顶的lca,也就是2,是有用的,那么我们现在就要把18弹掉,换成2,然后再扔进去一个16。
接下来我们要加一个20,那么它与栈顶的lca为2。我们就考虑16,16是没用的,把它弹掉,然后看见2,正好就是lca,就保留。
类似这样我们可以发现开始把所有询问点加入虚树后,我们把询问点按dfs序排个序,这时栈里面应该维护一个奇怪的玩意,先计算一个新加的点与栈顶的lca,然后如果一个栈里的东西一直都“没用”,也就是深度比这个lca来得大,就一直弹出栈顶,最后如果栈顶不是lca,就把lca加入栈,并且加入虚树,然后再加入这个点。
这样我们就可以求出虚树啦,同时我们也可以得到虚树上每一个点的父亲节点。
(友情提示:下文的某些地方可能会用控制点来代替最近点,反正就是一个意思)
接下来我们考虑如何求出虚树上每个点被哪个点控制。我们可以用一个pair<int,int>来存它到控制点的距离和控制点,然后我们用每一个点更新它的父亲,再用每一个父亲更新它的孩子。注意到因为所有虚树上的点的lca也在虚树上,所以对于虚树上某一个点和某一个控制点,第一遍必然会更新到lca,第二遍必然会更新到这个点,所以这个做法是正确的。
然后我们要考虑虚树以外的点要怎么维护。
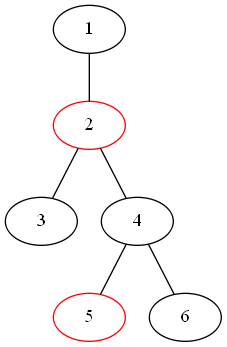
比如对于这样一个小树,红色的点在虚树上。
我们考虑虚树上的一条父子边,对应实际的树上就会是一坨东西。比如这棵树上2-5就对应4和6。
具体地说,对于一条父子边(f,x),f=fa[x],那么对应实际树上的就是f在x方向的这棵子树除掉x这棵子树。
例如2-5就表示4这棵子树除掉5这棵子树,就是4和6这两个点。
我们发现树上除了这些父子边,还有一些没有被计入统计的点,需要分别考虑,虚树根往上的都需要单独统计,例如1,还有像图中的3这样也不会被统计到。
注意到跟这些点最近的点必然和和这些点相连的点最近的是同一个点,比如1和3最近的都与2最近的一样。
现在,如果5与2最近的是同一个点,那么4和6必然也是这一个点。
否则我们可以发现,这是与深度有关的。比如2最近的点->2距离为p,5最近的点->5距离为q。
那么与控制5的点距离不超过(p+q+2到5距离)/2的点都应该选择5最近的点,那么深度就要>=dep[5]-(near_dis(2)+near_dis(5)+dis(2,5))/2+near_dis(5)。
只要从5开始往上跳到这个深度,计算一下就可以了。
需要注意的是,如果(p+q+2到5距离)是偶数的话,一定会有一个(些)点到2和5最近的点距离相同,那么这个(些)点应该选编号小的一个。即因为正常情况下这些点会选择下面那个点的控制点,所以如果上面那个点控制点编号小,就要考虑深度++。
所以基本的思路都清楚了,我们只要写一个倍增维护一下lca和往上跳这种东西就可以了。复杂度大概是O((n+q+∑m)logn)的。
代码终于写完啦~感人肺腑
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <math.h> #include <set> #include <map> using namespace std; int inf=1000000000; #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pob #define pc(x) putchar(x) namespace ib {char b[100];} inline void pint(int x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } #define SZ 666666 #define D 20 #define _els ;else //real tree namespace rt { int n,fst[SZ],nxt[SZ],vb[SZ],fa[SZ],up[SZ][D],dep[SZ],M=0,dfsn[SZ],C=0,sz[SZ]; void ad_de(int a,int b) {++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b;} void adde(int a,int b) {ad_de(a,b); ad_de(b,a);} void dfs(int p) { dfsn[p]=++C; sz[p]=1; for(int e=fst[p];e;e=nxt[e]) { int b=vb[e]; if(b==fa[p]) continue; fa[b]=up[b][0]=p; dep[b]=dep[p]+1; dfs(b); sz[p]+=sz[b]; } } void build() { dfs(1); for(int g=1;g<D;g++) { for(int i=1;i<=n;i++) { if(up[i][g-1]) up[i][g]=up[up[i][g-1]][g-1]; } } } //jump up (x=fa[x]) until dep[x]=d int jmp(int x,int d) { for(int i=D-1;i>=0;i--) { if(!up[x][i]||dep[up[x][i]]<d)_els x=up[x][i]; } return x; } int lca(int x,int y) { if(dep[x]>dep[y]) swap(x,y); y=jmp(y,dep[x]); if(x==y) return x; for(int i=D-1;i>=0;i--) { if(up[x][i]!=up[y][i]) x=up[x][i], y=up[y][i]; } return fa[x]; } } //virtual tree namespace vt { #define f_ first #define s_ second typedef pair<int,int> pii; //vs: points in vtree int sn,ss[SZ],vn,vs[SZ],stn=0,st[SZ],vfa[SZ],emp[SZ],vfe[SZ],anss[SZ],ss_[SZ]; pii ks[SZ]; //(dis,controller) bool cmp_dfsn(int a,int b) {return rt::dfsn[a]<rt::dfsn[b];} void build() { vn=stn=0; for(int i=1;i<=sn;i++) ss_[i]=ss[i]; //backup sort(ss+1,ss+1+sn,cmp_dfsn); for(int i=1;i<=sn;i++) vs[++vn]=ss[i], ks[ss[i]]=pii(0,ss[i]), anss[ss[i]]=0; for(int i=1;i<=sn;i++) { int x=ss[i]; if(!stn) {st[++stn]=x; vfa[x]=0; continue;} int lca=rt::lca(x,st[stn]); for(;rt::dep[st[stn]]>rt::dep[lca];--stn) { if(rt::dep[st[stn-1]]<=rt::dep[lca]) vfa[st[stn]]=lca; } if(st[stn]!=lca) { vs[++vn]=lca; ks[lca]=pii(inf,0); vfa[lca]=st[stn]; st[++stn]=lca; } vfa[x]=lca; st[++stn]=x; } //注意到按dfs序排序是满足儿子一定在父亲的后面的 sort(vs+1,vs+1+vn,cmp_dfsn); for(int i=1;i<=vn;i++) { int x=vs[i]; emp[x]=rt::sz[x]; if(i>1) vfe[x]=rt::dep[x]-rt::dep[vfa[x]]; } for(int i=vn;i>1;i--) { int x=vs[i],f=vfa[x]; ks[f]=min(pii(ks[x].f_+vfe[x],ks[x].s_),ks[f]); } for(int i=2;i<=vn;i++) { int x=vs[i],f=vfa[x]; ks[x]=min(pii(ks[f].f_+vfe[x],ks[f].s_),ks[x]); } for(int i=1;i<=vn;i++) { int x=vs[i],f=vfa[x]; //树根往上的点 if(i==1) {anss[ks[x].s_]+=rt::n-rt::sz[x]; continue;} int f_p=rt::jmp(x,rt::dep[f]+1),cnt=rt::sz[f_p]-rt::sz[x]; emp[f]-=rt::sz[f_p]; //这一棵子树已经处理过了 if(ks[f].s_==ks[x].s_) {anss[ks[x].s_]+=cnt; continue;} int md=rt::dep[x]-(ks[f].f_+ks[x].f_+vfe[x])/2+ks[x].f_; if((ks[f].f_+ks[x].f_+vfe[x])%2==0&&ks[f].s_<ks[x].s_) ++md; int dsz=rt::sz[rt::jmp(x,md)]-rt::sz[x]; //down_sz anss[ks[x].s_]+=dsz; anss[ks[f].s_]+=cnt-dsz; } for(int i=1;i<=vn;i++) anss[ks[vs[i]].s_]+=emp[vs[i]]; for(int i=1;i<=sn;i++) { pint(anss[ss_[i]]); pc(' '); } pc(10); } } int main() { rt::n=gi; for(int i=1;i<rt::n;i++) { int x=gi,y=gi; rt::adde(x,y); } rt::build(); int q=gi; while(q--) { vt::sn=gi; for(int i=1;i<=vt::sn;i++) vt::ss[i]=gi; vt::build(); } }