网络流例题学习2

有点长…分个P好了

人民群众喜闻乐见的网络流24题 http://cojs.tk/cogs/problem/index.php?key=%E7%BD%91%E7%BB%9C%E6%B5%8124%E9%A2%98

①搭配飞行员

二分图最大匹配裸题

如果要强行上最大流…那么就S->左边每一个点连边容量1，该连的边连一下容量1，右边每一个点->T连边容量1

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <limits>
#include <set>
#include <map>
using namespace std;
int n,fst[233333],nxt[233333],vb[233333],M=0,match[233333];
void ad_dl(int a,int b) {++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b;}
void addl(int a,int b) {ad_dl(a,b); ad_dl(b,a);}
bool vis[233333];
bool find(int x)
{
    for(int e=fst[x];e;e=nxt[e])
    {
        int b=vb[e];
        if(vis[b]) continue;
        vis[b]=1;
        if(!match[b]||find(match[b]))
        {
            match[b]=x; match[x]=b; return 1;
        }
    }
    return 0;
}
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} 
int main()
{
    FO(flyer)
    int n1;
    scanf("%d%d",&n,&n1);
    int a,b;
    while(scanf("%d%d",&a,&b)!=EOF) addl(a,b);
    int ans=0;
    for(int i=1;i<=n1;i++)
    {
        for(int j=1;j<=n;j++) match[j]=0;
        if(find(i)) ++ans;
    }
    printf("%d",ans);
}

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <limits>
#include <set>
#include <map>
using namespace std;
#define SZ 233333
int n,M=1;typedef long long ll;
int fst[SZ],nxt[SZ],vb[SZ],cap[SZ];
void _ad_dl(int a,int b,int c) {++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;cap[M]=c;}
void ad_dl(int a,int b,int c) {_ad_dl(a,b,c); _ad_dl(b,a,0);}
int S,T,q[SZ],d[SZ];
bool bfs()
{
    memset(d,-1,sizeof(d));
    d[S]=0; q[1]=S; int h=1,t=2;
    while(h!=t)
    {
        int cur=q[h++];
        for(int e=fst[cur];e;e=nxt[e])
        {
            int b=vb[e];
            if(d[b]==-1&&cap[e]) d[b]=d[cur]+1, q[t++]=b;
        }
    }
    return d[T]!=-1;
}
int dfs(int x,int f)
{
    if(f<=0) return 0;
    if(x==T) return f;
    int ca=0;
    for(int e=fst[x];e;e=nxt[e])
    {
        int b=vb[e];
        if(d[b]!=d[x]+1) continue;
        int w=dfs(b,min(cap[e],f-ca));
        cap[e]-=w; cap[e^1]+=w; ca+=w;
        if(ca==f) break;
    }
    if(!ca) d[x]=-1;
    return ca;
}
#define inf 1000000000
int dinic()
{
    int ans=0;
    while(bfs()) ans+=dfs(S,inf);
    return ans;
}
//=============以上均为模板=============
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
int main()
{
    FO(flyer)
    int n1;
    scanf("%d%d",&n,&n1);
    int a,b; S=n+1; T=n+2;
    while(scanf("%d%d",&a,&b)!=EOF) ad_dl(a,b,1), ad_dl(b,a,1);
    for(int i=1;i<=n1;i++) ad_dl(S,i,1);
    for(int i=n1+1;i<=n;i++) ad_dl(i,T,1);
    n+=2; printf("%d
",dinic());
}

②太空飞行计划

最大权闭合子图的裸题

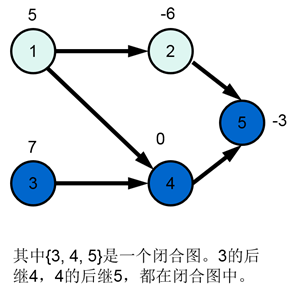
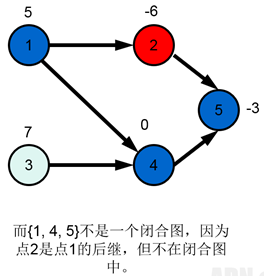
有向图的闭合图：闭合图内任意点的任意后继也一定还在闭合图中。

（以上两张图截自2007《最小割模型在信息学竞赛中的应用》Amber）

那这题我们把每一个仪器的点权设为-费用，实验点权设为收益，然后实验->仪器加边，这样就是要求一个点权最大的闭合子图。

转化成最小割：加一个源汇，源->正权点容量为点权，负权点->汇容量为-点权，原来的边容量为∞。然后只要选S割集的点就是最大权闭合子图，最大权值就是正权之和-最大流。

最小割=最大流这不用说吧。最小割的方案对于最大流来说只要从S开始在残余网络上bfs，能bfs到的是一个割集。

所以就是道大水题啦~

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <limits>
#include <set>
#include <map>
using namespace std;
#define SZ 233333
int n,M=1;typedef long long ll;
int fst[SZ],nxt[SZ],vb[SZ],cap[SZ];
void _ad_dl(int a,int b,int c) {++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;cap[M]=c;}
void ad_dl(int a,int b,int c) {_ad_dl(a,b,c); _ad_dl(b,a,0);}
int S,T,q[SZ],d[SZ];
bool bfs()
{
    memset(d,-1,sizeof(d));
    d[S]=0; q[1]=S; int h=1,t=2;
    while(h!=t)
    {
        int cur=q[h++];
        for(int e=fst[cur];e;e=nxt[e])
        {
            int b=vb[e];
            if(d[b]==-1&&cap[e]) d[b]=d[cur]+1, q[t++]=b;
        }
    }
    return d[T]!=-1;
}
int dfs(int x,int f)
{
    if(f<=0) return 0;
    if(x==T) return f;
    int ca=0;
    for(int e=fst[x];e;e=nxt[e])
    {
        int b=vb[e];
        if(d[b]!=d[x]+1) continue;
        int w=dfs(b,min(cap[e],f-ca));
        cap[e]-=w; cap[e^1]+=w; ca+=w;
        if(ca==f) break;
    }
    if(!ca) d[x]=-1;
    return ca;
}
#define inf 1000000000
int dinic()
{
    int ans=0;
    while(bfs()) ans+=dfs(S,inf);
    return ans;
}
//=============以上均为模板=============
int C[233333],P[233333];
char buf[2333333];
bool vis[2333333];
bool gj[2333333];
void bfs_2()
{
    int h=1,t=2; q[1]=S; gj[S]=1;
    while(h!=t)
    {
        int cur=q[h++];
        for(int e=fst[cur];e;e=nxt[e])
        {
            int b=vb[e];
            if(cap[e]&&!gj[b]) q[t++]=b, gj[b]=1;
        }
    }
}
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
int main()
{
    FO(shuttle)
    int tot=0,M,N; scanf("%d%d
",&M,&N);
    n=M+N+2; S=n-1; T=n;
    for(int i=1;i<=M;i++)
    {
        scanf("%d",P+i);
        tot+=P[i];
        ad_dl(S,i,P[i]);
        for(;;)
        {
            char c;
            do c=getchar(); while (c==' ');
            ungetc(c,stdin);
            if (c==10 || c==13) break;
            int x;
            scanf("%d",&x);
            ad_dl(i,x+M,1000000000);
        }
    }
    for(int i=1;i<=N;i++)
    {
        scanf("%d",C+i);
        ad_dl(i+M,T,C[i]);
    }
    int ans=dinic(); bfs_2();
    int f1=0;
    for(int i=1;i<=M;i++) if(gj[i])
    {
        if(f1) putchar(' '); else f1=1;
        printf("%d",i);
    }
    f1=0;
    putchar(10);
    for(int i=1;i<=N;i++) if(gj[i+M])
    {
        if(f1) putchar(' '); else f1=1;
        printf("%d",i);
    }
    putchar(10);
    printf("%d
",tot-ans);
}

这题输入较为捉鸡，然后去看std，get了一个新函数叫ungetc，就是把一个字符退回到输入流…(╯‵□′)╯为什么我原来不知道有这种神奇的函数

③最小路径覆盖问题

把一个顶点拆成两个，一个入点，一个出点，对于原图每一条边(i,j)，就把i的出点连到j的入点，然后二分图最大匹配，然后我们发现只要沿着匹配边查找到的都是一个路径上的点，输出所有路径就行。然后最小路径覆盖的条数就是顶点数-匹配数。

匈牙利的话输方案暴力dfs即可。dinic的话比较蛋疼，不太好描述……参见程序

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <vector>
#include <limits>
#include <set>
#include <map>
using namespace std;
#define SZ 666666
int N,M=1,fst[SZ],nxt[SZ],vb[SZ],cap[SZ],S,T;
void _ad_dl(int a,int b,int c) {++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; cap[M]=c;}
void ad_dl(int a,int b,int c)
{
    _ad_dl(a,b,c); _ad_dl(b,a,0);
}
int d[SZ],q[SZ];
bool bfs()
{
    for(int i=1;i<=N;i++) d[i]=-1;
    int h=0,t=1; q[0]=S; d[S]=0;
    while(h!=t)
    {
        int cur=q[h++];
        for(int e=fst[cur];e;e=nxt[e])
        {
            int b=vb[e],c=cap[e];
            if(!c||d[b]!=-1) continue;
            d[b]=d[cur]+1; q[t++]=b;
        }
    }
    return d[T]!=-1;
}
int dfs(int x,int f)
{
    if(f<=0) return 0;
    if(x==T) return f;
    int used=0;
    for(int e=fst[x];e;e=nxt[e])
    {
        int b=vb[e],c=cap[e];
        if(d[b]!=d[x]+1) continue;
        int cur=dfs(b,min(f-used,c));
        used+=cur; cap[e]-=cur; cap[e^1]+=cur;
        if(used==f) break;
    }
    return used;
}
int dinic()
{
    int ans=0;
    while(bfs()) ans+=dfs(S,1000000000);
    return ans;
}
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
int from[SZ],st[SZ],stn=0;
int main()
{
    FO(path3)
    int n,m; scanf("%d%d",&n,&m);
    N=n*2+2; S=N-1; T=N;
    //对于点x，入点为x+n，出点为x
    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        ad_dl(a,b+n,1);
    }
    for(int i=1;i<=n;i++) ad_dl(S,i,1), ad_dl(i+n,T,1);
    int ans=dinic();
    for(int i=1;i<=n;i++)
    {
        for(int e=fst[i];e;e=nxt[e])
        {
            if(!cap[e]&&!(e&1)) {from[i]=vb[e]-n; break;}
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int e=fst[i+n];e;e=nxt[e])
        {
            if(cap[e]&&!(e&1)) {st[++stn]=i; break;}
        }
    }
    for(int i=1;i<=stn;i++)
    {
        printf("%d",st[i]);
        int cur=from[st[i]];
        while(cur)
        {
            printf(" %d",cur);
            cur=from[cur];
        }
        putchar(10);
    }
    printf("%d
",n-ans);
}