先贴一点字符串相关算法好了。
学习资料:
《后缀数组——处理字符串的有力工具》罗穗骞
这是cxjyxx_me神犇的小结
其实上面的材料都说得很清楚了…为了复(骗)习(访)算(问)法(量)就写一写好了。
先说后缀数组本体,我们假设字符串叫s,长度为len,字符串从0开始存储。
首先我们先定义suffix(p)=s[p]…s[len-1]。
我们定义sa和rank。sa是一个0~n-1的排列满足suffix(sa[0])<suffix(sa[1])<…<suffix(sa[n-1]),就是n个后缀从小到大排序后的开头顺序排成一个序列。rank[i]保存的是suffix(i)从小到大的名次(即sa[rank[i]]=i)。
后缀数组是存在O(n)的做法的(当然比O(n)更低复杂度的做法并没有什么卵用),但是太难写了,所以在oi中更常用的是O(nlogn)甚至O(nlog^2n)的。
log?我们考虑倍增。
对于第i次比较,我们只考虑s[x]…s[min(x+2^(i-1)-1,len-1)]的子串,即从x开始往后2^(i-1)这么长,或者到字符串结尾。
例如bdabdc,第一次比较我们考虑b、d、a、b、d、c,第二次考虑bd、da、ab、bd、dc、c,第三次考虑bdab、dabd、abdc、bdc、dc、c,第四次考虑bdabdc、dabdc、abdc、bdc、dc、c。
我们发现”bdab”=”bd”+”ab”,”dabd”=”da”+”bd”,”bdabdc”=”bdab”+”dc”…就是说我们每一次对后缀的排序相当于对上一次的后缀排序进行双关键字排序(如果前半段不同比较前半段,否则比较后半段)!
所以如果我们直接每一次对上一次的结果双关键字sort一下…就可以做到O(nlog^2n)啦!
下面这份代码中rank只用来比较,所以中间过程中可能会有一样的rank,最后的rank才是真正的rank,然后sort时比较rank即可。
//codevs1500 //O(nlog^2n) #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <limits> #include <set> #include <map> using namespace std; #define SZ 666666 int n,sa[SZ],t[SZ],rank[SZ]; char s[SZ]; int p; bool cmp(int a,int b) {return (t[a]<t[b])||(t[a]==t[b]&&t[a+p]<t[b+p]);} bool same(int a,int b) {return t[a]==t[b]&&t[a+p]==t[b+p];} void getsa() { for(int i=0;i<n;i++) rank[i]=s[i]; for(int j=0;j<=n;(!j)?(j=1):(j=j+j)) { p=j; for(int i=0;i<n;i++) sa[i]=i, t[i]=rank[i]; sort(sa,sa+n,cmp); for(int i=0,p=0;i<n;i++) rank[sa[i]]=(i>0&&same(sa[i],sa[i-1]))?p:++p; } } int main() { scanf("%*d%s",s); n=strlen(s); getsa(); for(int i=0;i<n;i++) printf("%d ",sa[i]+1); }
为什么是O(nlog^2n)的呢?废话,有一个sort啊。
嗯好,那么O(nlogn)是什么做法呢?基数排序(又叫计数排序)!
但是我们需要先解决一个问题…基数排序如何双关键字?
在我们的印象中…基数排序就是对于每个数,找到有多少个数不大于它。
怎么找呢?前缀和啊。
但是为了解决相等的情况,每次我们取出一个数的时候都要把前缀和数组-1。
类似这样(摘自维基百科https://zh.wikipedia.org/wiki/%E8%AE%A1%E6%95%B0%E6%8E%92%E5%BA%8F)
代码写出来像这样:
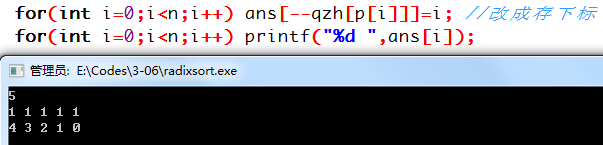
//基数排序 #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <limits> #include <set> #include <map> using namespace std; int n,p[2333333],qzh[2333333],ans[2333333]; int main() { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%d",p+i), ++qzh[p[i]]; for(int i=1;i<=1000000;i++) qzh[i]+=qzh[i-1]; for(int i=0;i<n;i++) ans[--qzh[p[i]]]=p[i]; for(int i=0;i<n;i++) printf("%d ",ans[i]); }
咦我们会发现一个问题,那就是对于相等的元素,位置前面的会放到比较后面的位置!
这是为什么呢?仔细想想你会觉得十分显然,因为顺着循环p[i],所以相等的元素,位于后面的元素此时的qzh[p[i]]因为前面减过会比较小,就会存在前面的位置。
所以我们发现如果我们改成倒着循环,在值一样的时候下标小的就会在前面。
所以假设我们要对a和b双关键字排序,a优先。那么我们先按b排序,然后倒着循环对a排序,就可以实现双关键字排序啦!
我们考虑把上面一段代码的sort改成双关键字的基数排序。当然,一般的字符串题字符集都比较小,如果实在比较大也只能sort…
那我们现在要做的就是先按第二关键字排序,再按第一关键字排序。所以就可以得到一个O(nlogn)的算法啦!
在放代码之前呢,再讲一个height数组好了。我们定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀。
那么对于j和k,如果rank[j]<rank[k],则suffix(j)和suffix(k)的最长公共前缀为height[rank[j]+1],height[rank[j]+2],height[rank[j]+3],…,height[rank[k]]中的最小值。(不会证…但是似乎挺显然的)
那么要如何求出height数组呢?height数组有如下性质:height[rank[i]]>=height[rank[i-1]]-1。那么我们根据这个性质按rank顺序求height就可以达到O(n)了。(要证明?翻论文啊233
代码是UOJ35 后缀排序(要求sa和height),需要注意的是代码里面求sa的时候要把n+1。类似这样:![]()
//uoj35 后缀排序 //O(nlogn) #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <limits> #include <set> #include <map> using namespace std; #define SZ 666666 int n,sa[SZ],t[SZ],rank[SZ],qzh[SZ],tmpsa[SZ],tmpr[SZ],h[SZ]; char s[SZ]; bool same(int a,int b,int p) {return t[a]==t[b]&&t[a+p]==t[b+p];} void getsa(int n,int m=233) { for(int i=0;i<n;i++) rank[i]=s[i], ++qzh[rank[i]]; for(int i=1;i<m;i++) qzh[i]+=qzh[i-1]; for(int i=n-1;i>=0;i--) sa[--qzh[rank[i]]]=i; for(int j=1;j<=n;j<<=1) { int cur=-1; for(int i=n-j;i<n;i++) tmpsa[++cur]=i; for(int i=0;i<n;i++) if(sa[i]>=j) tmpsa[++cur]=sa[i]-j; for(int i=0;i<n;i++) tmpr[i]=rank[tmpsa[i]]; for(int i=0;i<m;i++) qzh[i]=0; for(int i=0;i<n;i++) ++qzh[tmpr[i]]; for(int i=1;i<m;i++) qzh[i]+=qzh[i-1]; for(int i=n-1;i>=0;i--) t[i]=rank[i], sa[--qzh[tmpr[i]]]=tmpsa[i]; m=0; for(int i=0;i<n;i++) rank[sa[i]]=(i>0&&same(sa[i],sa[i-1],j))?m:++m; ++m; } for(int i=0;i<n;i++) rank[sa[i]]=i; } void geth(int n) { int p=0; for(int i=0;i<n;i++) { if(p) --p; int ls=sa[rank[i]-1]; while(s[ls+p]==s[i+p]) p++; h[rank[i]]=p; } } int main() { scanf("%s",s); n=strlen(s); getsa(n+1); geth(n); for(int i=1;i<=n;i++) printf("%d ",sa[i]+1); putchar(10); for(int i=2;i<=n;i++) printf("%d ",h[i]); }
我来解释一下代码好了~
调用的时候n是字符串长度(+1),m是字符集大小。
for(int i=0;i<n;i++) rank[i]=s[i], ++qzh[rank[i]]; for(int i=1;i<m;i++) qzh[i]+=qzh[i-1]; for(int i=n-1;i>=0;i--) sa[--qzh[rank[i]]]=i;
这段就是把开始的字符串排序,就是正常的基数排序。
for(int j=1;j<=n;j<<=1)
int cur=-1; for(int i=n-j;i<n;i++) tmpsa[++cur]=i; for(int i=0;i<n;i++) if(sa[i]>=j) tmpsa[++cur]=sa[i]-j;
开始按第二关键字排序。如果是开头为n-j~n-1这些段,因为它们没有后面一段,所以是最小的。然后排好序的后缀如果>=j,那么就可以作为一个后缀的后面一段。
for(int i=0;i<n;i++) tmpr[i]=rank[tmpsa[i]]; for(int i=0;i<m;i++) qzh[i]=0; for(int i=0;i<n;i++) ++qzh[tmpr[i]]; for(int i=1;i<m;i++) qzh[i]+=qzh[i-1]; for(int i=n-1;i>=0;i--) t[i]=rank[i], sa[--qzh[tmpr[i]]]=tmpsa[i];
排好第二关键字后再按第一关键字基数排序。
m=0; for(int i=0;i<n;i++) rank[sa[i]]=(i>0&&same(sa[i],sa[i-1],j))?m:++m; ++m;
这段和之前一样,比较排序后的每一段大小,并且更新字符集。
for(int i=0;i<n;i++) rank[sa[i]]=i;
最后我们要更新一下rank,因为之前的rank可能有一样的。
height数组就是暴力更新,好像也没什么好说的。
例题下回再说~