Necklace of Beads
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1036 Accepted Submission(s): 373
Problem Description
Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 40 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there?
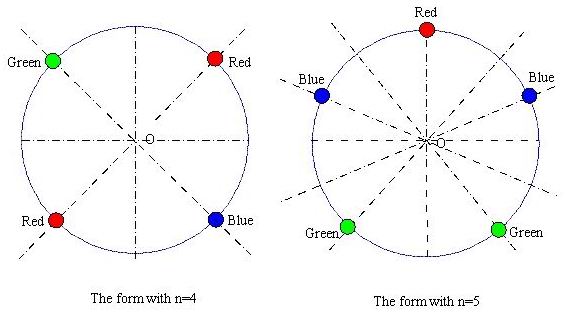

Input
The input has several lines, and each line contains the input data n.
-1 denotes the end of the input file.
-1 denotes the end of the input file.
Output
The output should contain the output data: Number of different forms, in each line correspondent to the input data.
Sample Input
4
5
-1
Sample Output
21
39
Source
三种颜色,对n个点围成的环着色,求不同的方案个数。
polya定理,置换一共有n*2个,n个是旋转,n个是翻转,翻转分奇偶讨论一下对称轴过点or不过点,计算出循环个数就好了。
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<map> 5 #include<set> 6 #include<vector> 7 #include<algorithm> 8 #include<cmath> 9 using namespace std; 10 #define LL long long 11 #define PI acos(-1.0) 12 LL thr[66]={1}; 13 int gcd(int a,int b){ 14 return b==0?a:gcd(b,a%b); 15 } 16 int main() 17 { 18 LL n,i,j; 19 for(i=1;i<=40;++i) thr[i]=thr[i-1]*3; 20 while(cin>>n){ 21 if(n==-1)break; 22 if(n==0){ 23 puts("0"); 24 continue; 25 } 26 LL ans=0; 27 for(i=1;i<=n;++i){ 28 ans+=thr[gcd(i,n)]; 29 } 30 if(n%2==0){ 31 ans=ans+thr[n/2]*(n/2); 32 ans=ans+thr[n/2+1]*(n/2); 33 } 34 else{ 35 ans=ans+thr[n/2+1]*n; 36 } 37 ans=ans/2; 38 ans=ans/n; 39 cout<<ans<<endl; 40 } 41 return 0; 42 }