题目描述
题目描述:
摩尔斯电码(又译为摩斯密码,Morse code)是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号。为了简单问题,去除所有的标点符号。
现在给你一段摩斯密码,请你把它们进行解密。
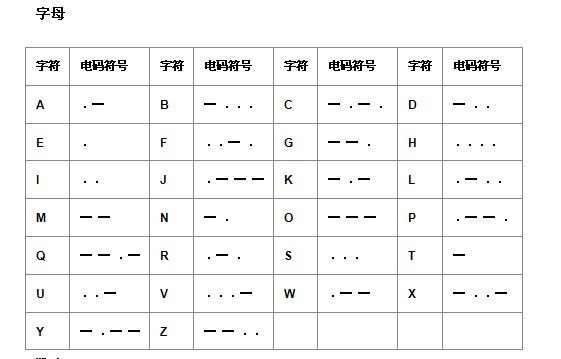
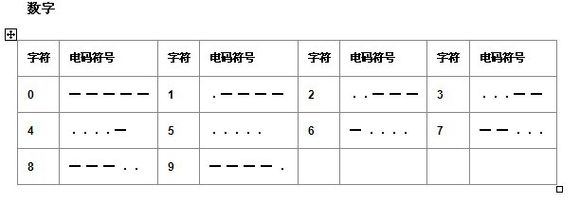
输入
含有T(T<=20)组数据,每组数据包含一段摩斯密码(由字符 '.' 和 '-' 以及 空格组成,连续空格个数不超过两个),每段占一行(不超过1000个字符),现在请你对他们进行解密;
输出
输出对应的解密后的结果(所有解密结果如果是英文字母一律输出小写英文字母),保证结果仅包含 数字 空格 字母。
样例输入
复制
5 .. . . . .. . .. .. .-.. --- ...- . -.-- --- ..-
样例输出
复制
i ee ei e i i love you
map跑一发,但不知道为啥格式错误最后随便改了改A了。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL unsigned long long 18 #define pii pair<int,int> 19 #define eps 1e-10 20 #define inf 0x3f3f3f3f 21 22 23 map<string,char>M; 24 void init(){ 25 M[".-"]='a';M["-..."]='b';M["-.-."]='c';M["-.."]='d'; 26 M["."]='e';M["..-."]='f';M["--."]='g';M["...."]='h'; 27 M[".."]='i';M[".---"]='j';M["-.-"]='k';M[".-.."]='l'; 28 M["--"]='m';M["-."]='n';M["---"]='o';M[".--."]='p'; 29 M["--.-"]='q';M[".-."]='r';M["..."]='s';M["-"]='t'; 30 M["..-"]='u';M["...-"]='v';M[".--"]='w';M["-..-"]='x'; 31 M["-.--"]='y';M["--.."]='z'; 32 M["-----"]='0';M[".----"]='1';M["..---"]='2';M["...--"]='3'; 33 M["....-"]='4';M["....."]='5';M["-...."]='6';M["--..."]='7'; 34 M["---.."]='8';M["----."]='9'; 35 } 36 char s[1100]; 37 int main() 38 { 39 LL n,m,i,j,k,t; 40 init(); 41 cin>>t; 42 getchar(); 43 while(t--){ 44 string ans=""; 45 string tmp=""; 46 gets(s); 47 LL l=strlen(s); 48 for(i=0;i<l;++i){ 49 if(s[i]==' '){ 50 ans+=M[tmp]; 51 tmp=""; 52 if(s[i+1]==' '){ 53 i++; 54 ans+=' '; 55 } 56 } 57 else{ 58 tmp+=s[i]; 59 } 60 } 61 ans+=M[tmp]; 62 for(int i=0;i<ans.length();++i){ 63 if(isalpha(ans[i])){ 64 ans[i]=tolower(ans[i]); 65 } 66 } 67 cout<<ans<<endl; 68 } 69 return 0; 70 } 71
题目描述
有一个N x M 大小的地图,地图中的每个单元包含一个大写字母。
若两个相邻的(这里的相邻指“上下左右”相邻)点上的字母相同,我们可以用线段连接这两个点。
若存在一个包含同一字母的环路,那么连接这些点我们可以得到一个多边形,
当且仅当多边形的边数大于等于4时,我们称这幅地图中存在“简单环路”。
现在给你一份地图,你来判断是否存在“简单环路”。
列如:
3 4
AAAA
ABCA
AAAA
字符“A”可以构成一个“简单环路”,其边数为4。
输入
第一行输入两个正整数n,m,2<=n,m<=50,分别表示地图的行列数。
接下来输入n行,每行m个大写字母。
输出
若存在“简单环路”输出“Yes”,否则输出“No”。
样例输入
复制
3 4 AAAA ABCA AADA
样例输出
复制
No
判断一个图中是否有环,刚开始想的用dfs感觉写起来很麻烦,最后用的并查集,每个格子看作一个点,注意一条边并一次就好,
发现两个同类点在一个集合中说明有环。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL unsigned long long 18 #define pii pair<int,int> 19 #define eps 1e-10 20 #define inf 0x3f3f3f3f 21 LL MOD=1e9+7; 22 23 char s[110][110]; 24 int e[110][110]; 25 26 int f[2600]; 27 int getf(int v){ 28 return f[v]==v?v:f[v]=getf(f[v]); 29 } 30 LL t,n,m,i,j,k; 31 struct Edge{ 32 int u,v,w; 33 }P[5050]; 34 int gid(int x,int y){ 35 return (x-1)*m+y; 36 } 37 int main() 38 { 39 40 while(cin>>n>>m){ 41 memset(e,0,sizeof(e)); 42 for(i=1;i<=n*m;++i) f[i]=i; 43 for(i=1;i<=n;++i) cin>>s[i]+1; 44 bool ok=0; 45 for(i=1;i<=n;++i){ 46 for(j=1;j<=m;++j){ 47 if(s[i][j]==s[i][j-1]){ 48 int u=gid(i,j),v=gid(i,j-1); 49 int fu=getf(u),fv=getf(v); 50 if(fu!=fv){ 51 f[fv]=fu; 52 } 53 else{ 54 ok=1; 55 break; 56 } 57 } 58 if(s[i][j]==s[i-1][j]){ 59 int u=gid(i,j),v=gid(i-1,j); 60 int fu=getf(u),fv=getf(v); 61 if(fu!=fv){ 62 f[fv]=fu; 63 } 64 else{//cout<<i<<' '<<j<<" "<<fu<<" "<<fv<<endl; 65 ok=1; 66 break; 67 } 68 } 69 if(ok) break; 70 } 71 if(ok) break; 72 } 73 ok?puts("Yes"):puts("No"); 74 } 75 return 0; 76 } 77 78 /* 79 .. .-.. --- ...- . -.-- --- ..--- 80 */ 81
C直接模拟。
题目描述
题意简单到令人发指!
序列A由N个整数组成,从中选出一个连续的子序列,使得这个子序列的和为正数,且和为所有和大于零的子序列中的最小值.
将这个值输出,若无解,输出no solution。
输入
第一行输入一个正整数N(2<N<50000)<n<50000)<n<50000)<n<50000)< div="">
第二行输入N个整数
输出
输出最小的正子段和
样例输入
复制
3 -1 2 3
样例输出
复制
1
贪心,考虑一下这段序列的和 sum[i,j]=SUM{a[i]+a[i+1]+...+a[j]},我们的目标是 MIN{sum[i,j]},也可以改写成MIN{pre[j]-pre[i-1]},转化成了前缀和的形式,问题转化为找到两个前缀和pre[a]和pre[b]满足 a<b且pre[a]<pre[b] 的最小的pre[b]-pre[a],对处理好的pre[]数组排序,枚举右边界i,如果i-1满足条件那显然i-1就是当前最优的,如果i-1不满足条件,在i-1前面有满足条件的k,那么让i-1和k配对会使得结果更优,所以我们只考虑相邻的点就可以了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 #define LL long long 7 pair<LL,int>sum[50010]; 8 int a[50010]; 9 int main() 10 { 11 int n,i,j; 12 cin>>n; 13 LL ans=9999999999; 14 for(i=1;i<=n;i++) cin>>a[i]; 15 for(i=1;i<=n;i++) { 16 sum[i].first=sum[i-1].first+a[i]; 17 sum[i].second=i; 18 } 19 sort(sum+1,sum+1+n); 20 if(sum[1].first>0)ans=sum[1].first; 21 for(i=2;i<=n;i++) { 22 if(sum[i].first>0) ans=min(ans,sum[i].first); 23 if(sum[i].second>sum[i-1].second && sum[i].first!=sum[i-1].first) ans=min(ans,sum[i].first-sum[i-1].first); 24 } 25 if(ans!=9999999999) cout<<ans<<endl; 26 else puts("no solution"); 27 return 0; 28 }
题目描述
广寒宫下有株二叉树,树上共有n个节点,通过n-1条树枝连接,树下有一只玉兔,吴刚提着斧子站在一旁。
他恼恨一切同他争夺嫦娥的事物,所以他决定通过砍二叉树上的n-1条树枝来毁掉这颗二叉树。
妙的是,这些树枝只能被砍一次,而且被砍后有一半的概率立即长出。
吴刚砍了n斧子后罢手了,他打算“不眠倚桂树”。你来猜猜,现在这株二叉树有多少联通块?(即联通块的期望值)
已知:最后一斧子砍了玉兔。
输入
输入一个正整数T(1<=T<=50)
接下来T行,每行输入一个正整数n,代表二叉树的节点数,2<=n<=1e5。
输出
输出联通块的期望值,答案的数据可能很大,所以输出答案乘2^(n-1)后再对1e9+7取模
样例输入
复制
1 2
样例输出
复制
3
提示
来源
直接根据题意列出来联通快个数分布律图,答案就是 { Σni=1(i*C(n-1,i-1)) }%1e9+7,由于组合数推到用到了除法需要取逆元,这里n不是很大,直接线性推导,inv[i]=(mod-mod/i)*inv[mod%i]%mod;记得中间取模防爆。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL unsigned long long 18 #define pii pair<int,int> 19 #define eps 1e-10 20 #define inf 0x3f3f3f3f 21 LL MOD=1e9+7; 22 LL inv[100100]={1,1}; 23 int main() 24 { 25 LL t,n,m,i,j,k; 26 for(i=2;i<100000;++i) 27 inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD; 28 scanf("%lld",&t); 29 while(t--){ 30 scanf("%lld",&n); 31 LL ans=1; 32 LL r=1; 33 for(i=1;i<n;++i){ 34 r=r*(n-i)%MOD*inv[i]%MOD; 35 ans+=(i+1)*r; 36 ans%=MOD; 37 } 38 cout<<ans<<endl; 39 } 40 return 0; 41 } 42
题目描述
我们把f(i)表示为i的正约数的和,而我们要求的是1<=i<=n之间所有i的f(i)之和!
输入
先输入一个正整数T,表示T个这是数据。T(T<=50)
每行输入一个正整数n。(n<10^6)
输出
输出一个数字,表示所求的数。
样例输入
复制
3 5 12 2018
样例输出
复制
21 127 3350309
1--n中因子x的个数就是floor(n/i);
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL unsigned long long 18 #define pii pair<int,int> 19 #define eps 1e-10 20 #define inf 0x3f3f3f3f 21 LL MOD=1e9+7; 22 23 24 LL cal(int n){ 25 LL r=n; 26 for(int i=2;i<=n;++i){ 27 r+=(n/i)*i; 28 } 29 return r; 30 } 31 int main(){ 32 int n,i,j,k; 33 cin>>k; 34 while(k--){ 35 scanf("%d",&n); 36 printf("%lld ",cal(n)); 37 } 38 return 0; 39 }
题目描述
伴随着科技的发展,我们的生活也越来越多姿多彩,随着手机的普及,各种交友软件也在快速的发展。
小a是个老实人,当然只是自己理解而已,其实小a是个不折不扣的渣男。因为他在有女朋友的同时,还在疯狂的撒网,利用各种交友软件寻求更适合自己的伴侣。
小a女朋友当然不是省油的灯,自然了解小a的本性,所以在每次见面时就会翻看小a的软件记录,来了解小a近期的状况,机智的小a当然会在女朋友来之前就给完全清理干净了。
终于在某次时间紧急的情况下,小a的软件记录并不一定能够完全删除,但是小a知道,自己每个软件记录的火热程度以及最终删除时间(即可以删除的最晚时间,过时将无法删除)。每个软件记录的删除需要一分钟,软件记录的火热程度,正好对应着女朋友的刺激值,小a想知道,在有限的时间内,如何才能够让女朋友的刺激值最小,求出最小值。
输入
第一行一个正整数T。表示样例个数(0<T<10)
每组有两个整数n,m,分别表示一共有n个软件以及女朋友到来的时间(0<n<=10^5,0<m<=10^6)
往下对应着n行,每行有两个正整数e,f分别对应每个软件记录的火热程度和该软件的最终删除时间。(0<e<=10^5,0<f<=10^6)
题目中涉及到的时间全部以分钟为单位。
输出
输出对女朋友的最小刺激值;结果占一行。
样例输入
复制
2 4 2 20 1 10 1 30 2 40 2 6 2 20 1 10 1 30 2 40 2 50 3 60 3
样例输出
复制
30 100
贪心,考虑每个时间x,在这个时间点能销毁的软件的时间属性必须>=x,大的时间肯定不会影响小时间,倒序往堆里push节点每次pop队首就好了。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL unsigned long long 18 #define pii pair<int,int> 19 #define eps 1e-10 20 #define inf 0x3f3f3f3f 21 LL MOD=1e9+7; 22 23 struct node{ 24 int a,b; 25 bool operator<(const node& tmp)const{ 26 return a<tmp.a; 27 } 28 }P[100010]; 29 bool cmpb(node A,node B){ 30 return A.b>B.b; 31 } 32 priority_queue<node>q; 33 int main() 34 { 35 LL t,n,m,i,j,k; 36 cin>>t; 37 while(t--){ 38 while(!q.empty()) q.pop(); 39 scanf("%lld%lld",&n,&m); 40 LL sum=0,ans=0; 41 for(i=1;i<=n;++i){ 42 scanf("%d%d",&P[i].a,&P[i].b); 43 sum+=P[i].a; 44 } 45 sort(P+1,P+1+n,cmpb); 46 for(i=m,j=1;i>=1;--i){ 47 while(j<=n&&P[j].b>=i) 48 q.push(P[j++]); 49 if(!q.empty()){ 50 ans+=q.top().a; 51 q.pop(); 52 } 53 } 54 cout<<sum-ans<<endl; 55 } 56 return 0; 57 }
H-dp+矩阵幂
原题bzoj1009,只不过这道题限制了可以转移的字母状态
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 #include<bits/stdc++.h> 13 using namespace std; 14 #define mp make_pair 15 #define pb push_back 16 #define debug puts("debug") 17 #define LL long long 18 #define ULL unsigned long long 19 #define uint unsigned int 20 #define pii pair<int,int> 21 #define eps 1e-10 22 #define inf 0x3f3f3f3f 23 24 char s1[155],s2[155]; 25 LL mod=(LL)1<<32; 26 struct matrix{ 27 int len; 28 LL a[66][66]; 29 matrix(){ 30 memset(a,0,sizeof(a)); 31 } 32 matrix operator*(matrix& tmp){ 33 matrix ans; 34 ans.len=len; 35 for(int i=0;i<=len;++i){ 36 for(int j=0;j<=len;++j){ 37 for(int k=0;k<=len;++k){ 38 ans.a[i][k]+=a[i][j]*tmp.a[j][k]; 39 ans.a[i][k]%=mod; 40 } 41 } 42 } 43 return ans; 44 } 45 46 void show(){ 47 puts("------------------------------------"); 48 for(int i=0;i<=len;++i){ 49 for(int j=0;j<=len;++j){ 50 cout<<a[i][j]<<' '; 51 } 52 cout<<endl; 53 } 54 puts("------------------------------------"); 55 } 56 }A,I; 57 matrix qpow(matrix X,int n){ 58 matrix ans=I; 59 while(n){ 60 if(n&1) ans=ans*X; 61 X=X*X; 62 n>>=1; 63 } 64 return ans; 65 } 66 int t,n,m,i,j,k; 67 int f[66]; 68 void solve(){ 69 int l1=strlen(s1+1),l2=strlen(s2+1); 70 A.len=I.len=l2; 71 memset(A.a,0,sizeof(A.a)); 72 for(i=0;i<=l2;++i) I.a[i][i]=1; 73 f[0]=0,f[1]=0; 74 for(i=2;i<=l2;++i){ 75 j=f[i-1]; 76 while(j&&s2[j]!=s2[i-1]) j=f[j]; 77 f[i]=j+1; 78 } 79 for(i=0;i<l2;++i){ 80 for(j=1;j<=l1;++j){ 81 k=i+1; 82 while(k&&s1[j]!=s2[k]) k=f[k]; 83 A.a[i][k]++; 84 A.a[i][k]%=mod; 85 } 86 } 87 88 A.a[l2-1][l2]=0; 89 //A.show(); 90 matrix ans=qpow(A,n); 91 LL res=0; 92 for(i=0;i<l2;++i) res=(res+ans.a[0][i])%mod; 93 cout<<res<<endl; 94 } 95 int main(){ 96 97 scanf("%d",&t); 98 while(t--){ 99 scanf("%d%s%s",&n,s1+1,s2+1); 100 solve(); 101 } 102 return 0; 103 } 104 /* 105 3 106 3 107 ab 108 ab 109 4 110 acd 111 ca 112 113 5 114 ab 115 aaa 116 */
I,b-a;
题目描述
每个人 都有自己独有的计数方式 比如以下 字符串111123455可以表示为4个1,1个2,1个3,1个4,2个5.为了方便记忆就表示为4--1,1--2,1--3,1--4,2--5当然顺序肯定不能变换 计数方式可以表示为“a--b”的形式 在计数方式中相连的b互不相等且a与b不为0 独有的计数方式 如果转化为字符串 字符串的长度小于10的9次方
给你下面的计数方式 例如5--4也就是字符串44444,10--4也就是字符串4444444444
给你这样的计数方式 判断这个字符串中有多少连续子串所构成的整数是4的倍数
例如5--4可表示为字符串44444里面共有(4,4,4,4,4,44,44,44,44,444,444,444,4444,4444,44444)15个是4的倍数;
输入
第一行是数字T(T<1000)<t<100) 表示下面有t组实例<="" h3="">
每一行一个独有的计数方式 长度小于100
<t<100) 表示下面有t组实例<="" h3="">
输出
输出字符串中有多少个是4的倍数 占一行
样例输入
复制
4 5--4 1--1,1--2 2--4,2--2,2--3 1--4,1--3,1--2,1--1
样例输出
33
打表查一下4的倍数的数字会发现规律,对于个位数,只有4/8是4的倍数,对于多位数,如果个位是奇数那他不可能是4的倍数,
如果
个位数是0/4/8,那十位数只有是偶数,这个数才是4的倍数;如果个位数是2/6那么十位数只有是奇数这个数才是4的倍数。
知道规律就简单了,记录下pre表示前面几段有多少个数字,枚举一下当前段的数字,奇数不管,2/6就加上pre,4/8根据前面的
数的奇偶性分情况讨论一下。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 #define LL long long 7 #define uint unsigned int 8 9 10 LL a[110],b[110]; 11 char s[110]; 12 int main() 13 { 14 int i,j,k,t; 15 16 scanf("%d",&t); 17 getchar(); 18 while(t--){ 19 int tot=0; 20 gets(s); 21 LL ans=0,pre=0; 22 23 LL n=strlen(s),tmp=0; 24 s[n]=','; 25 for(i=0;i<=n;++i){ 26 if(isdigit(s[i])){ 27 tmp=tmp*10+(s[i]-'0'); 28 } 29 else if(s[i]=='-'){ 30 i++; 31 tot++; 32 a[tot]=tmp; 33 tmp=0; 34 } 35 else if(s[i]==','){ 36 b[tot]=tmp; 37 tmp=0; 38 } 39 } 40 for(i=1;i<=tot;++i){ 41 42 43 if(b[i]==2||b[i]==6){ 44 if(b[i-1]%2==1){ 45 ans+=pre; 46 } 47 } 48 else if(b[i]==4||b[i]==8){ 49 if(b[i-1]%2==0){ 50 ans+=a[i]*(pre+pre+a[i]+1)/2; 51 } 52 else{ 53 ans+=a[i]*(pre+pre+a[i]+1)/2; 54 ans=ans-pre; 55 } 56 } 57 pre+=a[i]; 58 } 59 cout<<ans<<endl; 60 } 61 return 0; 62 } 63