利用dfs生成树求解,dfn[u]用于维护当前节点时间戳,low[u]维护当前节点能访问到得最小时间戳(祖先)。
注意这里的low[u]是指当前节点指向其祖先时才可以更新,如果是指向的兄弟则不可以,此时这二点不可能在一个scc中。
low[u] 为u 或u的子树能够追溯到的最早的栈中节点的次序号 .,栈中节点一定是u得祖先。
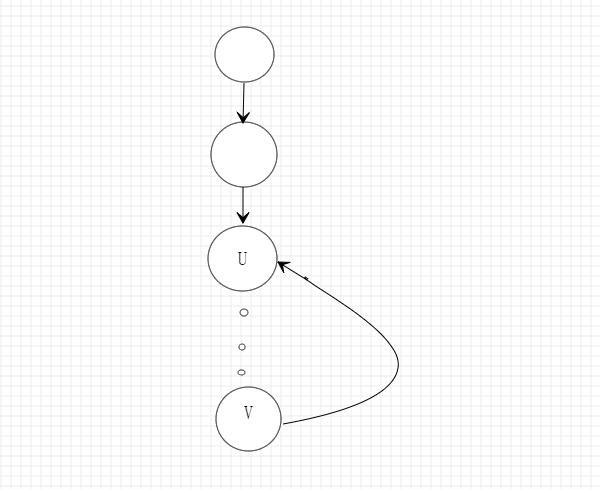
按照dfs得方式会生成dfs树,算法的思想就是在回溯得过程中把SCC一个一个得找到。如上图所示,如果存在一个SCC,那个在对应的dfs树中这些节点一定位于一条树链上,
树这个东西特殊性在于只要加上一条边就出现了环,如果V指向U且low[u]==dfn[u],那么显然U...V构成的环是一个SCC;所以说这个算法的关键一个是更新low数组,一个是从栈中
弹出SCC两步。如果未出现low[u]==dfn[u]那么说明low[u]<dfn[u],即u可以再往上走形成一个更大的环,他们才属于一个SCC。
1 void dfs(int u){ 2 dfn[u]=low[u]=++cnt; 3 S.push(u); 4 for(int v:g[u]){ 5 if(!dfn[v]){ 6 dfs(v); 7 low[u]=min(low[u],low[v]); 8 }else if(!scc[v]){ 9 low[u]=min(low[u],dfn[v]); //注意这里是v还在栈中时才更新,如果不在栈中说明已经有了scc,没必要更新,会出错导致scc无法正确得出。这句话也就防止了上述得指向兄弟操作。 10 } 11 } 12 if(low[u]==dfn[u]){ 13 ++scc_cnt; 14 int x=-1; 15 for(;;){ 16 x=S.top();S.pop(); 17 scc[x]=scc_cnt; 18 if(x==u)break; 19 } 20 } 21 }
模板prob:http://acm.hdu.edu.cn/showproblem.php?pid=1269
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int maxn=10005; 5 vector<int>g[maxn]; 6 stack<int>S; 7 int N,M,cnt,scc_cnt; 8 int low[maxn],dfn[maxn],scc[maxn]; 9 void dfs(int u){ 10 dfn[u]=low[u]=++cnt; 11 S.push(u); 12 for(int v:g[u]){ 13 if(!dfn[v]){ 14 dfs(v); 15 low[u]=min(low[u],low[v]); 16 }else if(!scc[v]){ 17 low[u]=min(low[u],dfn[v]); 18 } 19 } 20 if(low[u]==dfn[u]){ 21 ++scc_cnt; 22 int x=-1; 23 for(;;){ 24 x=S.top();S.pop(); 25 scc[x]=scc_cnt; 26 if(x==u)break; 27 } 28 } 29 } 30 int main(){ 31 while(cin>>N>>M){ 32 if(N==0&&M==0)break; 33 int A,B; 34 cnt=scc_cnt=0; 35 for(int i=1;i<=N;++i)g[i].clear(),dfn[i]=low[i]=scc[i]=0; 36 while(!S.empty())S.pop(); 37 for(int i=1;i<=M;++i){ 38 cin>>A>>B; 39 g[A].push_back(B); 40 } 41 for(int i=1;i<=N;++i){ 42 if(!dfn[i]){ 43 dfs(i); 44 } 45 } 46 cout<<(scc_cnt==1?"Yes":"No")<<endl; 47 } 48 return 0; 49 }