• CSP-201312

     桶来一下就好了。

     坑点是'X'，容易忽略掉。

     暴力可以A，但如果n过大就是以前做过的一道题目了，很经典。

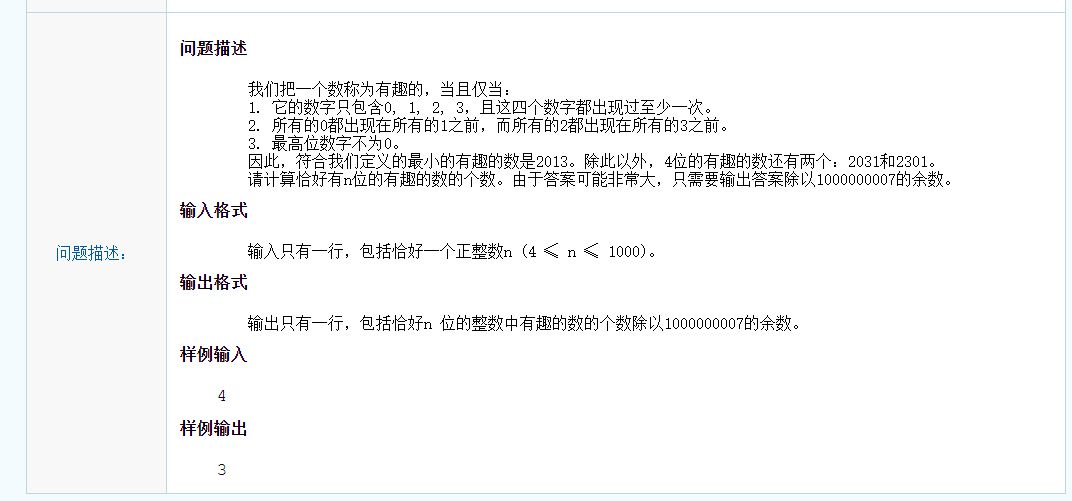
     状压dp做的，考虑f[i][k]表示进行到第k位，当前数字状态为k时方案个数，k只有2^4=16种状态，最后f[n][15]即为答案，1A了开心。由于这个破网站不保存代码所以没代码可贴= =

    试题编号： 201312-5
    试题名称： I’m stuck!
    时间限制： 1.0s
    内存限制： 256.0MB
    问题描述
    　　给定一个R行C列的地图，地图的每一个方格可能是'#', '+', '-', '|', '.', 'S', 'T'七个字符中的一个，分别表示如下意思：
    　　'#': 任何时候玩家都不能移动到此方格；
    　　'+': 当玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非'#'方格移动一格；
    　　'-': 当玩家到达这一方格后，下一步可以向左右两个方向相邻的一个非'#'方格移动一格；
    　　'|': 当玩家到达这一方格后，下一步可以向上下两个方向相邻的一个非'#'方格移动一格；
    　　'.': 当玩家到达这一方格后，下一步只能向下移动一格。如果下面相邻的方格为'#'，则玩家不能再移动；
    　　'S': 玩家的初始位置，地图中只会有一个初始位置。玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非'#'方格移动一格；
    　　'T': 玩家的目标位置，地图中只会有一个目标位置。玩家到达这一方格后，可以选择完成任务，也可以选择不完成任务继续移动。如果继续移动下一步可以向上下左右四个方向相邻的任意一个非'#'方格移动一格。
    　　此外，玩家不能移动出地图。
    　　请找出满足下面两个性质的方格个数：
    　　1. 玩家可以从初始位置移动到此方格；
    　　2. 玩家不可以从此方格移动到目标位置。
    输入格式
    　　输入的第一行包括两个整数R 和C，分别表示地图的行和列数。(1 ≤ R, C ≤ 50)。
    　　接下来的R行每行都包含C个字符。它们表示地图的格子。地图上恰好有一个'S'和一个'T'。
    输出格式
    　　如果玩家在初始位置就已经不能到达终点了，就输出“I'm stuck!”（不含双引号）。否则的话，输出满足性质的方格的个数。
    样例输入
    5 5
    --+-+
    ..|#.
    ..|##
    S-+-T
    ####.
    样例输出
    2
    样例说明
    　　如果把满足性质的方格在地图上用'X'标记出来的话，地图如下所示：
    　　--+-+
    　　..|#X
    　　..|##
    　　S-+-T
    　　####X
    只有这一道留下了代码 。
    　　很容易想到对S和T分别BFS一下然后找满足条件得点。T有些特殊，他需要找一条倒着走得路，一开始我只考虑了.感觉其他符号都无所谓最后发现了问题，针对每一个方向考虑就好了。举个例子说明：假如当前向上走，那么下一步得格子不可以是'-'，一旦是'-'那么这条路反过来显然不可能成立，其他也同理把所有符号考虑下即可。
      1 #include<iostream>
  2 #include<bits/stdc++.h>
  3 using namespace std;
  4 #define LL long long 
  5 char e[55][55];
  6 int N,M;
  7 int Sx,Sy,Tx,Ty;
  8 bool f1[55][55],f2[55][55];
  9 int fx[4][2]={
 10 -1,0,
 11 1,0,
 12 0,-1,
 13 0,1
 14 };
 15 struct node{
 16     int x,y;
 17 };
 18 bool can(){
 19     memset(f1,0,sizeof(f1));
 20     queue<node>q;
 21     q.push(node{Sx,Sy});
 22     while(!q.empty()){
 23         node u=q.front();
 24         q.pop();
 25         int x=u.x,y=u.y;
 26         if(f1[x][y]==1)continue;
 27         f1[x][y]=1;
 28         if(e[x][y]=='S' || e[x][y]=='+'|| e[x][y]=='T'){
 29             for(int i=0;i<4;++i){
 30                 int dx=x+fx[i][0];;
 31                 int dy=y+fx[i][1];;
 32                 if(dx<1||dy<1||dx>N||dy>M||
 33                 e[dx][dy]=='#' || f1[dx][dy]==1)continue;
 34                 q.push(node{dx,dy});
 35             }
 36         }
 37         else if(e[x][y]=='-'){
 38                 for(int i=2;i<4;++i){
 39                 int dx=x+fx[i][0];;
 40                 int dy=y+fx[i][1];;
 41                 if(dx<1||dy<1||dx>N||dy>M||
 42                 e[dx][dy]=='#' || f1[dx][dy]==1)continue;
 43                 q.push(node{dx,dy});
 44             }
 45         }
 46         else if(e[x][y]=='|'){
 47                 for(int i=0;i<2;++i){
 48                 int dx=x+fx[i][0];;
 49                 int dy=y+fx[i][1];;
 50                 if(dx<1||dy<1||dx>N||dy>M||
 51                 e[dx][dy]=='#' || f1[dx][dy]==1)continue;
 52                 q.push(node{dx,dy});
 53             }
 54         }
 55         else if(e[x][y]=='.'){
 56                 for(int i=1;i<2;++i){
 57                 int dx=x+fx[i][0];;
 58                 int dy=y+fx[i][1];;
 59                 if(dx<1||dy<1||dx>N||dy>M||
 60                 e[dx][dy]=='#' || f1[dx][dy]==1)continue;
 61                 q.push(node{dx,dy});
 62             }
 63         }
 64     }
 65     return f1[Tx][Ty];
 66 }
 67 void gao1(){
 68     memset(f2,0,sizeof(f2));
 69     queue<node>q;
 70     q.push(node{Tx,Ty});
 71     while(!q.empty()){
 72         node u=q.front();
 73         q.pop();
 74         int x=u.x,y=u.y;
 75         if(f2[x][y]==1)continue;
 76         f2[x][y]=1;
 77         for(int i=0;i<4;++i){
 78             int dx=x+fx[i][0];
 79             int dy=y+fx[i][1];
 80             if(dx<1||dy<1||dx>N||dy>M||
 81                 e[dx][dy]=='#' || f2[dx][dy]==1)continue;
 82             if(i==0){
 83                 if(e[dx][dy]=='+'||e[dx][dy]=='|'||e[dx][dy]=='.'||e[dx][dy]=='S'||e[dx][dy]=='T')
 84                 q.push(node{dx,dy});
 85             }else if (i==1){
 86                 if(e[dx][dy]=='+'||e[dx][dy]=='|'||e[dx][dy]=='S'||e[dx][dy]=='T')
 87                 q.push(node{dx,dy});
 88             }else if (i==2){
 89                 if(e[dx][dy]=='+'||e[dx][dy]=='-'||e[dx][dy]=='S'||e[dx][dy]=='T')
 90                 q.push(node{dx,dy});
 91             }else{
 92                 if(e[dx][dy]=='+'||e[dx][dy]=='-'||e[dx][dy]=='S'||e[dx][dy]=='T')
 93                 q.push(node{dx,dy});
 94             }
 95         }
 96     }
 97 }
 98 int main(){
 99     cin>>N>>M;
100     for(int i=1;i<=N;++i)cin>>e[i]+1;
101     for(int i=1;i<=N;++i){
102         for(int j=1;j<=M;++j){
103             if(e[i][j]=='S'){
104                 Sx=i,Sy=j;
105             }
106             if(e[i][j]=='T'){
107                 Tx=i,Ty=j;
108             }
109         }
110     }
111     if(can()==0)cout<<"I'm stuck!"<<endl;
112     else{
113         gao1();
114         int ans=0;
115         for(int i=1;i<=N;++i){
116             for(int j=1;j<=M;++j){
117                 if(f1[i][j]==1&&f2[i][j]==0)ans++;
118             }
119         }
120         cout<<ans<<endl;
121     }
122     return 0;
123 }
  • 相关阅读:
    perl6中函数参数(2)
    perl6中函数参数(1)
    上传绕过(转载)
    perl6中的hash定义(1)
    mssql手工注入2
    mssql手工注入1
    mssql注入中的储存用法删除与恢复
    perl 复制exe文件的简单方法
    python shell
    perl中设置POST登录时的重定向
  • 原文地址：https://www.cnblogs.com/zzqc/p/12104633.html
Copyright © 2020-2023  润新知