后缀数组
定义
后缀:Suffix(i)表示从i到结尾的字串
后缀数组:SA[i]表示将字符串的每个后缀按字典序排序后第i小的后缀的下缀
排名:Rank[i]表示第i位开始的后缀经过排序后是第几小
做法
朴素做法O(n^2 log n)
倍增
先将第1位,第2位......第n位按大小排序(相同可以并列)
然后将第1位与第2位合并,第2位与第3位合并.....第n-1位与第n位合并
将合并完后的进行排序
之后再将第1~2位与第3~4位合并,第2~3位与第4~5位合并.......第n-3~n-2位与第n-1~n位合并
再排序
以此类推
贴个百度百科的图。。。
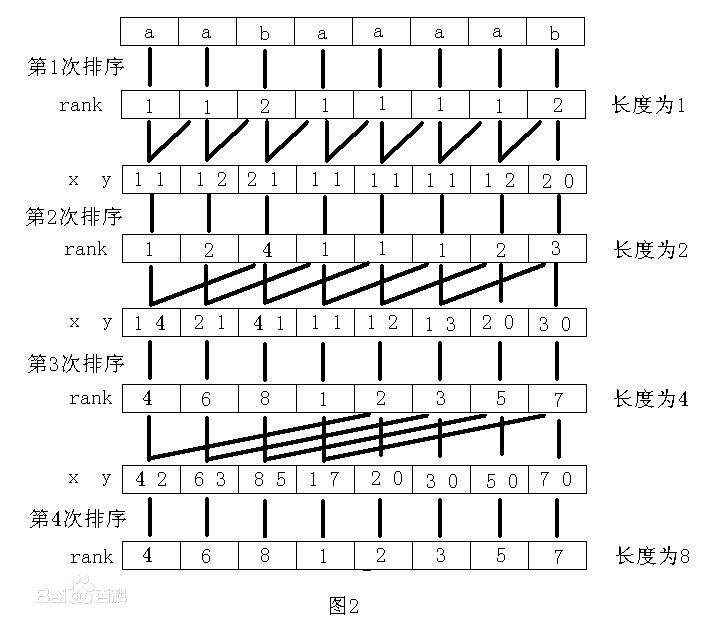
直到没有rank相同,结束
快排最坏O(n logn^2)
还是很慢。
我们注意到这里相当与在做两位数的排序,
所以我们就用
基数排序
每次排序O(n),总复杂度O(n log n)
简单说下做法
先按个位数丢到标号为0-9的桶里
串起来
再将十位数丢到标号为0-9的桶里
再串起来
以此类推
这里只要将“个位数”和“十位数”丢到编号为1-n的桶里就够了
代码待补....
最长公共前缀(Longest Common Prefix)
定义
定义LCP(i,j)表示Suffix(i)与Suffix(j)的最长公共前缀
定理
LCP(i,j)=LCP(j,i)
LCP(i,i)=len(Suffix(SA[i]))=n-SA[i]+1
LCP Lemma:对于∀j∈(i,k),1≤i<k≤n,都有LCP(i,k)=min(LCP(i,j),LCP(j,k))
证明:
设p=min(LCP(i,j),LCP(j,k)),u=Suffix(SA[i]),v=Suffix(SA[j]),w=Suffix(SA[k])
根据定义
u和v的前p个字符相等,v和w的前p个字符相等
所以u和w的前p个字符相等,LCP(i,k)≥p
不妨假设LCP(i,k)>p
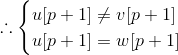 或
或 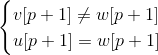
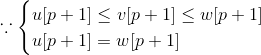
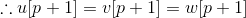
这与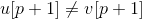 或
或 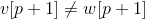 不符
不符
所以 LCP(i,k)=p
证毕
LCP Theorem:LCP(i,k)=min(LCP(j-1,j)) 1≤i<j≤k≤n
证明:
假设LCP(i,k-1)=min(LCP(j-1,j)) 1≤i<j≤k-1<n成立
因为LCP(i,k)=min(LCP(i,k-1),LCP(k-1,k))
所以LCP(i,k)=min(LCP(j-1,j)) 1≤i<j≤k≤n成立(数学归纳法)
证毕