所谓闭合子图就是给定一个有向图,从中选择一些点组成一个点集V。对于V中任意一个点,其后续节点都仍然在V中。比如:
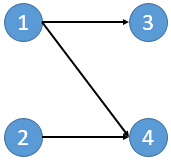
在这个图中有8个闭合子图:∅,{3},{4},{2,4},{3,4},{1,3,4},{2,3,4},{1,2,3,4}
小Ho:闭合子图我懂了,但是这跟我们这次的问题有啥关系呢?
小Hi:我们先把这次的问题转化为2分图。将N个活动看作A部,将M个学生看作B部。若第i个活动需要第j个学生,就连一条从A[i]到B[j]的有向边。比如对于例子:
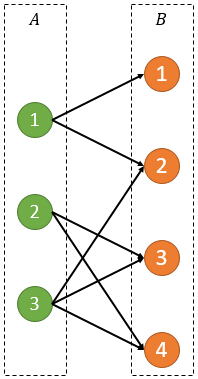
假如选择A[1],则我们需要同时选择B[1],B[2]。那么选择什么活动和其需要的学生,是不是就刚好对应了这个图中的一个闭合子图呢?
如果把活跃值算作权值,A部的节点包含有正的权值,B部的节点是负的权值。那么我们要求的也就是一个权值最大的闭合子图了?我们要求解的正是最大权闭合子图。它的求解方法是使用网络流,因此我们需要将这个图再进一步转化为网络流图。
对于一般的图来说:首先建立源点s和汇点t,将源点s与所有权值为正的点相连,容量为权值;将所有权值为负的点与汇点t相连,容量为权值的绝对值;权值为0的点不做处理;同时将原来的边容量设置为无穷大。举个例子:
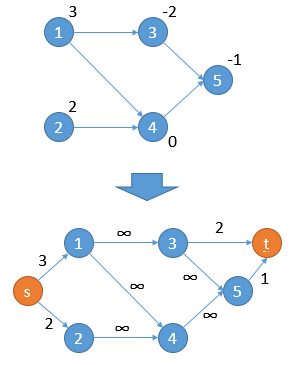
对于我们题目中的例子来说,其转化的网络流图为:

上图中黑边表示容量无穷大的边。
最大权闭合子图的权值等于所有正权点之和减去最小割。
接下来来证明这个结论,首先我们要证明两个引理:
1. 最小割一定是简单割
简单割指得是:割(S,T)中每一条割边都与s或者t关联,这样的割叫做简单割。
因为在图中将所有与s相连的点放入割集就可以得到一个割,且这个割不为正无穷。而最小割一定小于等于这个割,所以最小割一定不包含无穷大的边。因此最小割一定一个简单割。
2. 简单割一定和一个闭合子图对应
闭合子图V和源点s构成S集,其余点和汇点t构成T集。
首先证明闭合子图是简单割:若闭合子图对应的割(S,T)不是简单割,则存在一条边(u,v),u∈S,v∈T,且c(u,v)=∞。说明u的后续节点v不在S中,产生矛盾。
接着证明简单割是闭合子图:对于V中任意一个点u,u∈S。u的任意一条出边c(u,v)=∞,不会在简单割的割边集中,因此v不属于T,v∈S。所以V的所有点均在S中,因此S-s是闭合子图。
由上面两个引理可以知道,最小割也对应了一个闭合子图,接下来证明最小割就是最大权的闭合子图。
首先有割的容量C(S,T)=T中所有正权点的权值之和+S中所有负权点的权值绝对值之和。
闭合子图的权值W=S中所有正权点的权值之和-S中所有负权点的权值绝对值之和。
则有C(S,T)+W=T中所有正权点的权值之和+S中所有正权点的权值之和=所有正权点的权值之和。
所以W=所有正权点的权值之和-C(S,T)
由于所有正权点的权值之和是一个定值,那么割的容量越小,W也就越大。因此当C(S,T)取最小割时,W也就达到了最大权。