最大流最小割定理

对于一个割(S,T)，我们定义净流f(S,T)表示穿过割(S,T)的流量之和，即：

f(S,T) = Σf(u,v) | u∈S,v∈T

举个例子(该例子选自算法导论)：

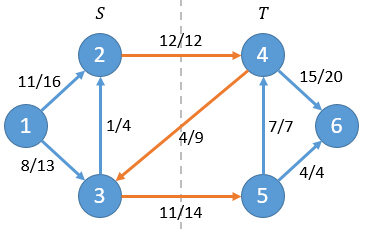
净流f = f(2,4)+f(3,4)+f(3,5) = 12+(-4)+11 = 19

同时我们定义割的容量C(S,T)为所有从S到T的边容量之和，即：

C(S,T) = Σc(u,v) | u∈S,v∈T

同样在上面的例子中，其割的容量为：

c(2,4)+c(3,5)=12+14=26

小Ho：也就是说在计算割(S,T)的净流f(S,T)时可能存在反向的流使得f(u,v)<0，而容量C(S,T)一定是非负数。

小Hi：你这么说也没错。实际上对于任意一个割的净流f(S,T)总是和网络流的流量f相等。比如上面例子中我们改变一下割的方式：

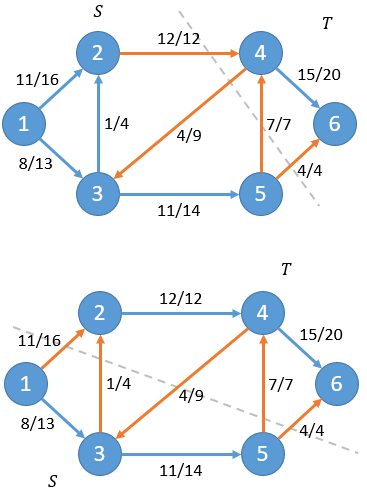
可以计算出对于这两种情况净流f(S,T)仍然等于19。

一个直观的解释是：根据网络流的定义，只有源点s会产生流量，汇点t会接收流量。因此任意非s和t的点u，其净流量一定为0，也即是Σ(f(u,v))=0。而源点s的流量最终都会通过割(S,T)的边到达汇点t，所以网络流的流f等于割的静流f(S,T)。

严格的证明如下：

f(S,T) = f(S,V) - f(S,S)
从S到T的流等于从S到所有节点的流减去从S到S内部节点的流
f(S,T) = f(S,V)
由于S内部的节点之间存在的流一定有对应的反向流，因此f(S,S)=0
f(S,T) = f(s,V) + f(S-s,V)
再将S集合分成源点s和其他属于S的节点
f(S,T) = f(s,V)
由于除了源点s以外其他节点不会产生流，因此f(S-s,V)=0
f(S,T) = f(s,V) = f

所以f(S,T)等于从源点s出来的流，也就是网络的流f。

小Ho：简单理解的话，也就是说任意一个割的净流f(S,T)都等于当前网络的流量f。

小Hi：是这样的。而对于任意一个割的净流f(S,T)一定是小于等于割的容量C(S,T)。那也即是，对于网络的任意一个流f一定是小于等于任意一个割的容量C(S,T)。

而在所有可能的割中，存在一个容量最小的割，我们称其为最小割。

这个最小割限制了一个网络的流f上界，所以有：

对于任一个网络流图来说，其最大流一定是小于等于最小割的。

小Ho：但是这和增广路又有什么关系呢？

小Hi：接下来就是重点了。利用上面讲的知识，我们可以推出一个最大流最小割定理：

对于一个网络流图G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：
1. 流f是图G的最大流
2. 残留网络Gf不存在增广路
3. 对于G的某一个割(S,T)，此时f = C(S,T)

首先证明1 => 2：

我们利用反证法，假设流f是图G的最大流，但是残留网络中还存在有增广路p，其流量为fp。则我们有流f'=f+fp>f。这与f是最大流产生矛盾。

接着证明2 => 3：

假设残留网络Gf不存在增广路，所以在残留网络Gf中不存在路径从s到达t。我们定义S集合为：当前残留网络中s能够到达的点。同时定义T=V-S。
此时(S,T)构成一个割(S,T)。且对于任意的u∈S,v∈T，有f(u,v)=c(u,v)。若f(u,v)<c(u,v)，则有Gf(u,v)>0，s可以到达v，与v属于T矛盾。
因此有f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)。

最后证明3 => 1：

由于f的上界为最小割，当f到达割的容量时，显然就已经到达最大值，因此f为最大流。

这样就说明了为什么找不到增广路时，所求得的一定是最大流。