卷积神经网络基础

卷积神经网络基础

feature map 大小计算

对于 Conv1d，Pytorch 的文档给出了如下的公式 1，对于二维和三维的情况是通用的。

[L_{out} = lfloor frac{ L_{in} + 2 imes padding - dilation imes (kernel\_size - 1) - 1 }{ stride } floor + 1 ag{1} ]

feature map 的大小由四个参数决定，分别是 kernel_size，padding，stride，dilation。下面逐个加上进行分析。

kernel_size

假设输入长度是 5，卷积核为 3，那么输出是 3。输入和输出的公式如下。

[L_{out} = L_{in} - kernel\_size + 1 ag{2} ]

padding

现在在原来的基础上加上 padding，假设在两边加 padding，其实就相当于增大输入的长度。

[L_{out} = L_{in} + 2 imes padding - kernel\_size + 1 ag{3} ]

stride

在上面的基础，再加上步长。默认的步长是 1，如果将步长变为 2，那么相当于直接减半。步长变为 3，那么除 3。举个例子，长度为 9，没有 padding，卷积核大小为 2。步长为 1，输出为 8。步长为 2，输出为 4，舍掉一个多余的输入。步长为 3，输出为 3。步长为 4，输出为 2，同样舍掉一个多余的输入。

[L_{out} = lfloor frac{ L_{in} + 2 imes padding - kernel\_size }{ stride } floor + 1 ag{4} ]

dilation

kernel 的元素之间的距离。默认是 1。假设卷积核大小为 3，dilation 为 2 时，卷积核大小会变成 5，dilation 为 3 时，卷积核大小会变成 7。假设卷积核大小为 5，dilation 为 2 时，卷积核大小会变成 9，dilation 为 3 时，会变成 (3 * 4) + 1 = 13。至此可以发现规律，卷积核原大小为 k，dilation 为 d，那么有 d * (k - 1) + 1，代入公式 4。

[L_{out} = lfloor frac{ L_{in} + 2 imes padding - dilation * (kernel\_size - 1) - 1 }{ stride } floor + 1 ag{5} ]

参数大小计算

《深度学习入门》一书中有如下卷积例子，对于一个 C 个通道，高度 H，宽度 W 的图片，经过滤波器，可以得到一个 (1, OH, OW) 的特征图。每个通道都有一个卷积核，C 个通道就有 C 个卷积核。所以卷积层的参数和通道数量成正比。

一般实现中，会有一个参数 out_channels，这个参数用于控制输出多少个通道。一个输出通道，需要一个不同的卷积核。所以参数量也和输出通道数量成正比。

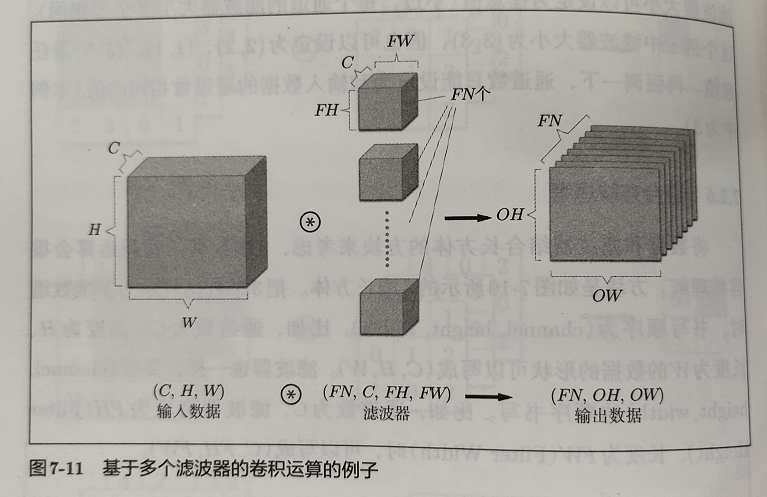
此外，卷积层一般还会有偏置量。每个输出通道一个偏置量。

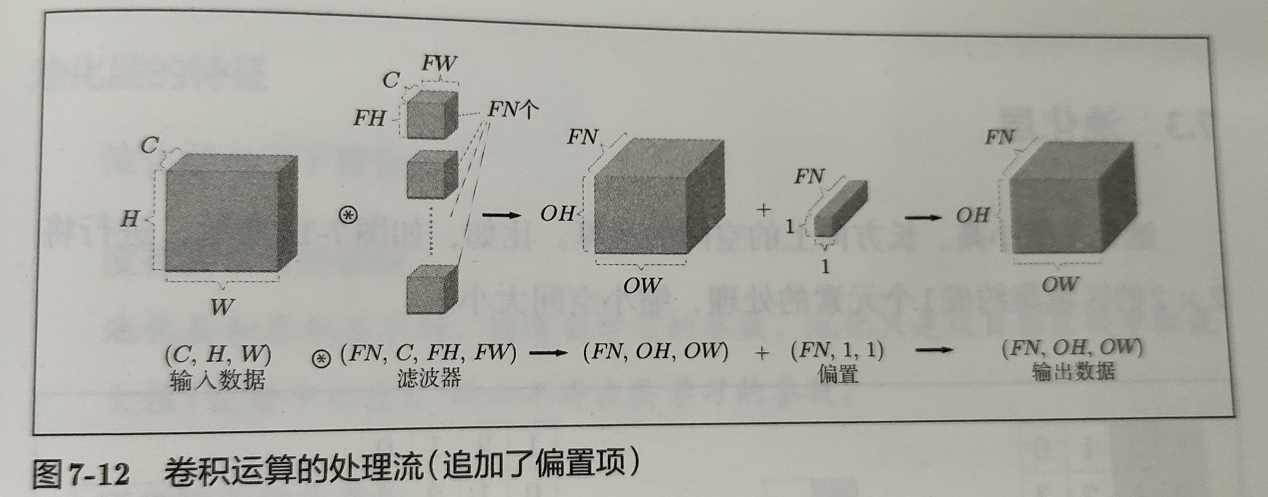
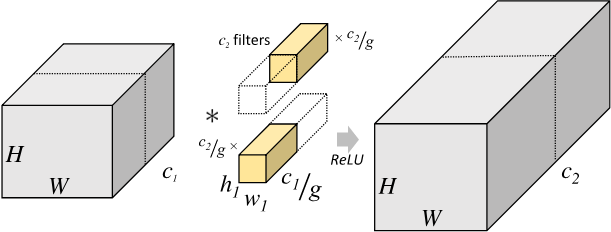
Pytorch 的文档还有一个 groups 参数，默认是 1。如果不是 1，那么需要进行分组卷积[2]。怎么分组呢？将输入和输出都分成 g 组，输入和输出的每一组对应上，然后算卷积核参数。输入和输出通道都要除以分组数，总的参数量还要乘以分组数。这么一分析，除两次，乘一次，参数量减少了 $frac{1}{g} $ ！

小结

参数量首先由卷积核决定，接着参数量和输入通道、输出通道都成正比，卷积层的偏置量参数和输出通道成正比。如果分组，那么参数量还要除以分组数量。

im2col

如果按照卷积的算法去老老实实计算，速度不会太快。一般使用 im2col 进行加速，用空间换时间，然后使用矩阵乘法来完成计算。将图片按照滤波器的应用区域依次展开成一行，卷积核展开成一列，接着就可以用矩阵乘法来进行卷积了。

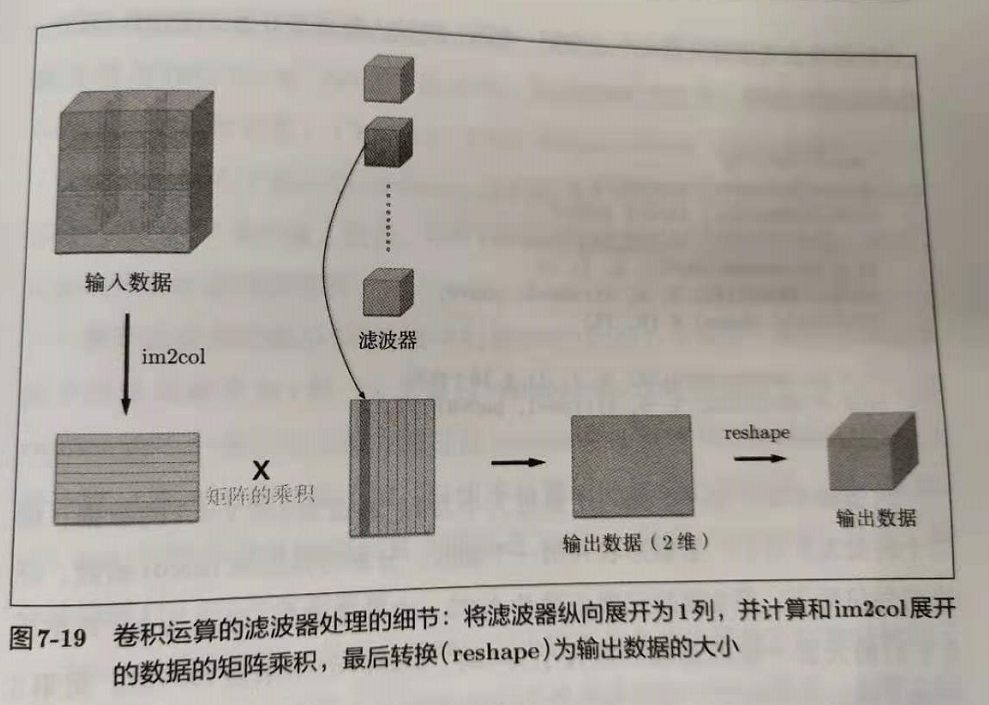
im2col 的输入是一个四维数据 (N, C, H, W)，输出是一个二维数组 ()。

实现

知乎上的一篇文章，将这个过程理了理，从一张图一个通道一个卷积核，逐步推理到多张图多个通道多个卷积，最后提供了一个实现。

核心是下面这一句代码：

col[y_start+x::outsize, :] = img[:, y_min:y_max, x_min:x_max, :].reshape(N, -1)

应该如何理解呢？

• 最终 col 是什么样子的？每个图片上，每个卷积到的局部区域，展开成向量，然后叠起来。一个图片有 N 行，那么加上 batch 就有 N * batch 那么多行。
• img 是 NHWC，C 放最后，img[:, y_min:y_max, x_min:x_max, :] 的结果是用卷积核圈出每个图片的局部构成的向量。注意这里取出来每个图片构成的局部向量，所以要分散放，设置步长为 outsize，然后分散放上去。

参考链接

[1] https://pytorch.org/docs/stable/generated/torch.nn.Conv1d.html
[2] https://zhuanlan.zhihu.com/p/65377955