双向链表（前插操作，删除操作）

循环单链表的出现，虽然能够实现从任一结点出发沿着链能找到其前驱结点，但时间耗费是O（n）。

如果希望从表中快速确定某一个结点的前驱，另一个解决方法就是在单链表的每个结点里再增加一个指向其前驱的指针域prior。

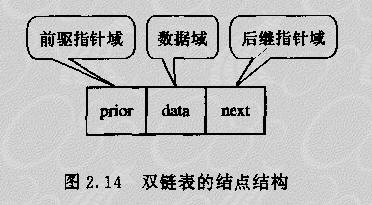
这样形成的链表中就有两条方向不同的链，我们可称之为双（向）链表（DoubleLinked List）。双链表的结构定义如下：

typedef structDNode

{

ElemType data;

struct DNode*prior,*next;

}DNode,*DoubleList;

与单链表类似，双链表一般也是有头指针唯一确定的，增加头结点也能使双链表的某些运算变得方便。同时双向链表也可以有循环表，称为双向循环链表，其结构如图2.15所示。

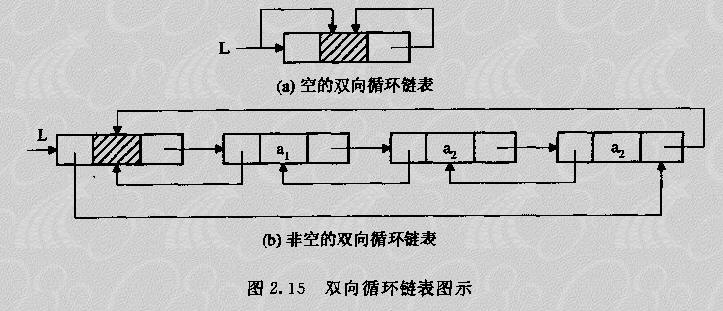
由于在双向链表中既有前向链又有后向链，寻找任一个结点的直接前驱结点与直接后继结点变得非常方便。设指针p指向双链表中某一结点，则有下式成立：

P->prior->next=p=p->next->prior

在双向链表中，那些只涉及后继指针的算法，如求表长度、取元素、元素定位等，与单链表中相应的算法相同，但对于前插和删除操作则涉及到前驱和后继两个方向的指针变化，因此与单链表中的算法不同。

1.双向链表的前插操作

算法描述：欲在双向链表第i个结点之前插入一个新的结点，则指针的变化情况如图2.16所示。

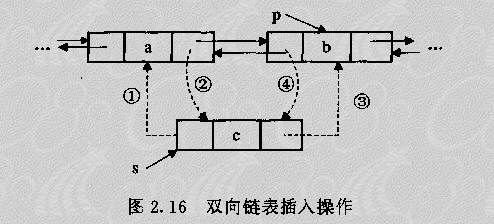
int DlinkIns(DoubleList L,int i,ElemType e)

{

 DNode *s,*p;

 …/*先检查待插入的位置i是否合法（实现方法同单链表的前插操作）*/

 …/*若位置i合法，则让指针p指向它*/

 s=(DNode *)malloc(sizeof(DNode));

 if(s)

   {

    s->data=e;

    s->prior=p->prior;p->prior->next=s;

    s->next=p;p->prior=s;

    return TRUE;

   }

 else

    teturn fALSE;

}

2.双向链表的删除操作

算法描述：欲删除双向链表中的第i个结点，则指针的变化情况如图2.17所示。

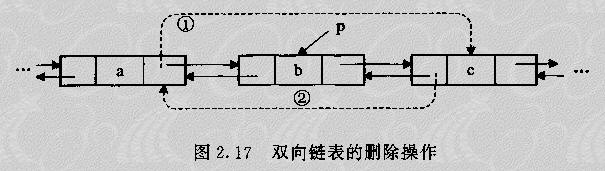
int DlinkDel(DoubleList L,int i,ElemType *e)

{

 DNode *p;

 …/*首先检查待插入的位置i是否合法（实现方法同单链表的删除操作）*/

 …/*若位置i合法，则让指针p指向它*/

 *e=p->prior->next=p->next;

 p->next->prior->p=p->prior;

 free(p);

 return TRUE;

}

转自：

https://blog.csdn.net/csdanca11/article/details/7173856