这题就是网络流的一个技巧,学会了就很好做了
以下连边默认是容量为1的。
考虑把牛拆成两个点,中间连容量为1的边,这样就保证了一头牛只会被经过一次(否则它可能享用很多食物)。前面的点(入点)负责连入边,后面的点(出点)负责连出边。从食物向入点连边,出点向饮料连边。另设超级源点s向食物连边,饮料向超级汇点t连边。
样例的图建好大概长这样
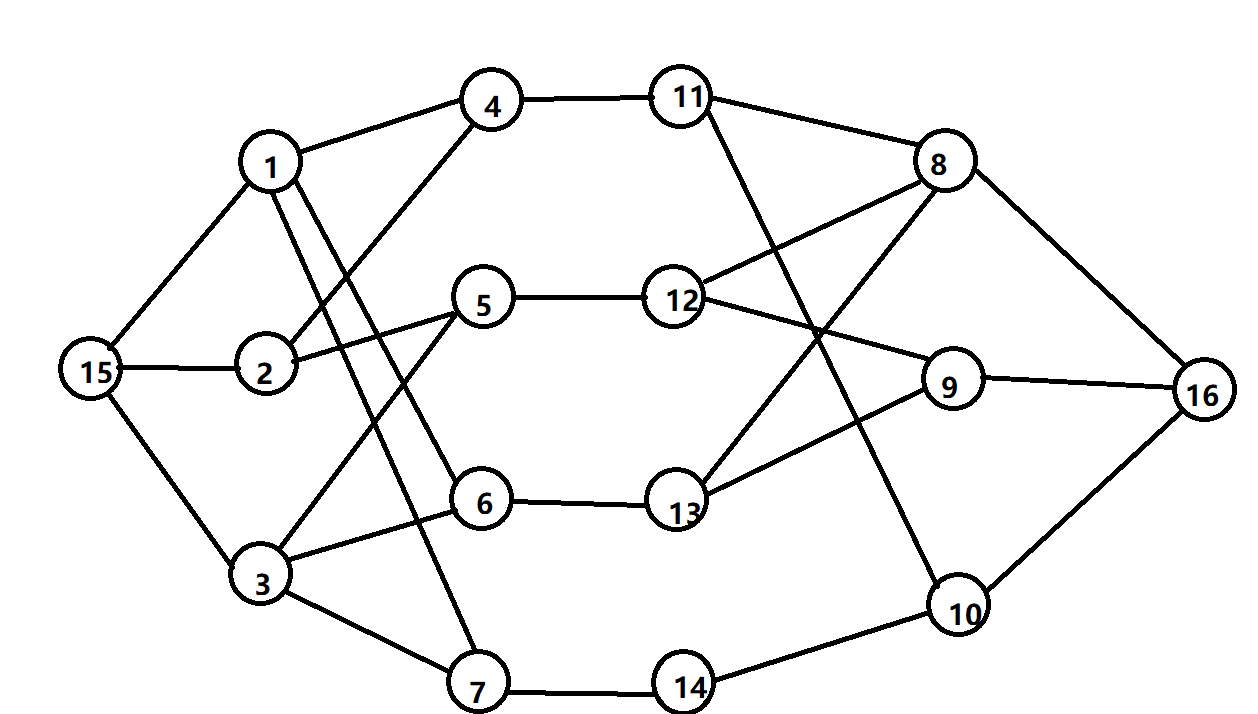
看完图应该就很好理解了。
代码特地放了注释。可以把注释符号删掉,看看连了那些边。
#include<bits/stdc++.h>
using namespace std;
const int N=420;
const int inf=1000000007;
int n,f,d,s,t,sum;
struct edge{
int nxt,val,to;
}e[21000*2];
int head[N],num_edge=1;
void add(int from,int to,int val)
{
++num_edge;
e[num_edge].nxt=head[from];
e[num_edge].to=to;
e[num_edge].val=val;
head[from]=num_edge;
}
bool inq[N];
int dep[N],cur[N];
bool bfs()
{
for(int i=1;i<=t;++i)
inq[i]=false,dep[i]=inf,cur[i]=head[i];
dep[s]=1;
queue<int>q;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();inq[u]=false;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(dep[v]>dep[u]+1&&e[i].val)
{
dep[v]=dep[u]+1;
if(!inq[v])inq[v]=true,q.push(v);
}
}
}
return dep[t]!=inf;
}
int maxflow;
int dfs(int u,int flow)
{
if(u==t){maxflow+=flow;return flow;}
int used=0,rlow;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(e[i].val&&dep[v]==dep[u]+1)
{
rlow=dfs(v,min(e[i].val,flow-used));
if(rlow)
{
used+=rlow;
e[i].val-=rlow;
e[i^1].val+=rlow;
}
if(used==flow)break;
}
}
return used;
}
void dinic()
{
while(bfs())dfs(s,inf);
}
int main()
{
scanf("%d%d%d",&n,&f,&d);
s=f+n+d+n+1;t=s+1;
for(int i=f+1;i<=f+n;++i)
add(i,i+n+d,1),add(i+n+d,i,0)/*,cout<<i<<" "<<i+n+d<<endl*/;
for(int i=1;i<=f;++i)
add(s,i,1),add(i,s,0)/*,cout<<s<<" "<<i<<endl*/;
for(int i=1;i<=d;++i)
add(i+f+n,t,1),add(t,i+f+n,0)/*,cout<<i+f+n<<" "<<t<<endl*/;
for(int i=1;i<=n;++i)
{
int fi,di;
scanf("%d%d",&fi,&di);
for(int j=1,x;j<=fi;++j)
{
scanf("%d",&x);
add(x,i+f,1),add(i+f,x,0)/*,cout<<x<<" "<<i+f<<endl*/;
}
for(int j=1,x;j<=di;++j)
{
scanf("%d",&x);
add(i+n+d+f,x+f+n,1),add(x+f+n,i+n+d+f,0)/*,cout<<i+n+d+f<<" "<<x+f+n<<endl*/;
}
}
dinic();
printf("%d\n",maxflow);
return 0;
}