线段树
- 了解线段树，什么线段树，线段树定义；
- 创建线段树；
- 线段树的维护；
- 线段树的查询；
- 题目练习；
核心：线段树维护的是区间信息！！！！
一、了解线段树 ：
题目一：
10000个正整数，编号1到10000，用A[1],A[2],A[10000]表示。
修改：无
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.
方法一：对于统计L,R ，需要求下标从L到R的所有数的和，从L到R的所有下标记做[L…R],问题就是对A[L…R]进行求和。这样求和，对于每个询问，需要将(R-L+1)个数相加。
方法二：更快的方法是求前缀和,令 S[0]=0, S[k]=A[1…k] ，那么，A[L…R]的和就等于S[R]-S[L-1]，这样，对于每个询问，就只需要做一次减法，大大提高效率。
题目二：
10000个正整数，编号从1到10000，用A[1],A[2],A[10000]表示。
修改：1.将第L个数增加C （1 <= L <= 10000）
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.
再使用方法二的话，假如A[L]+=C之后，S[L],S[L+1],S[R]都需要增加C,全部都要修改，见下表。
从上表可以看出，方法一修改快，求和慢。 方法二求和快，修改慢。
那有没有一种结构，修改和求和都比较快呢？答案当然是线段树。
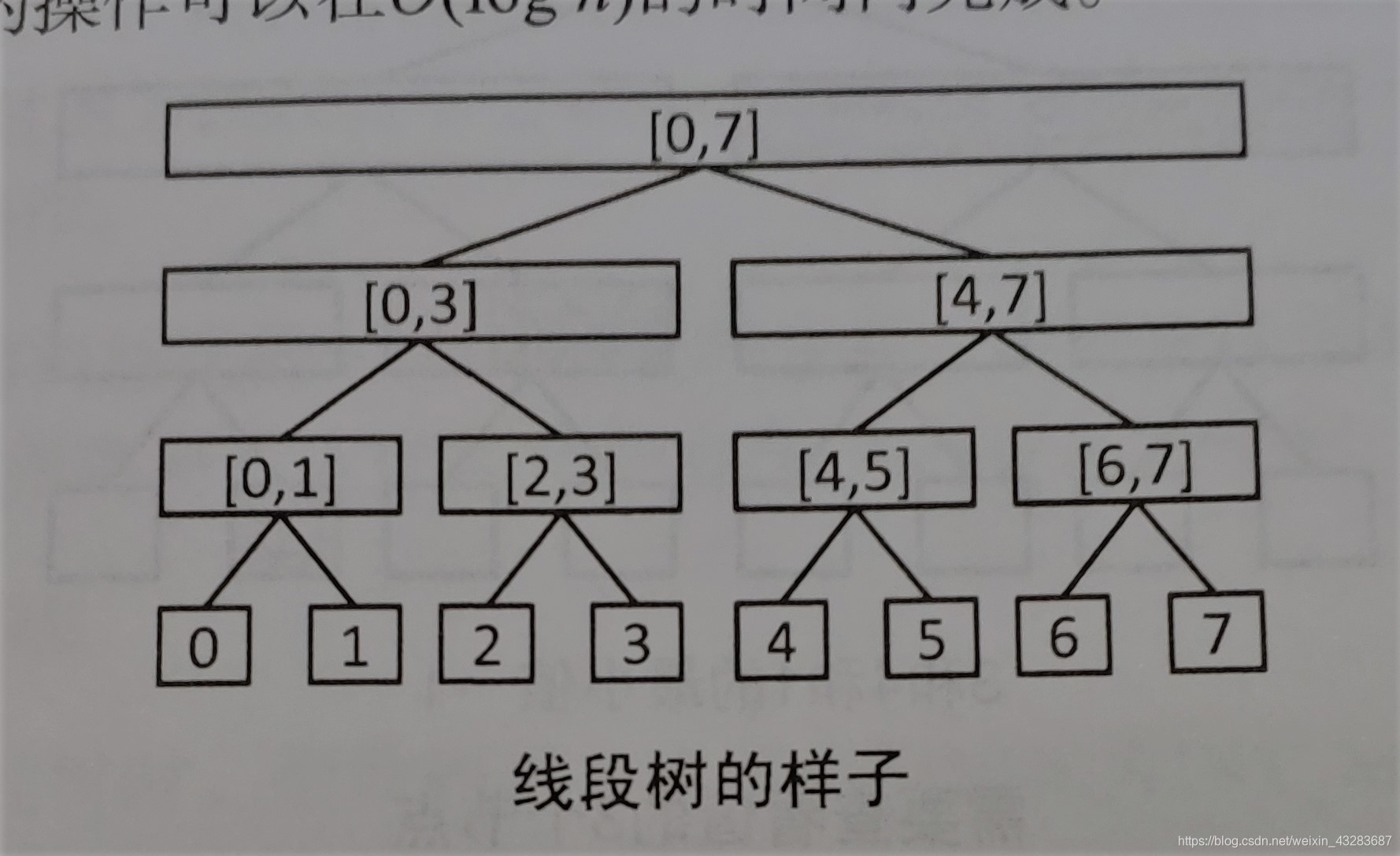官方解释：线段树分为两种：一种为自下而上的update（）；一种是自上而下的pushdown（）。
二、创建线段树：
void build(int l, int r, int rt)//建树
{
if(l == r)
{
sum[rt] = *值*;
return ;
}
int mid = (l + r) / 2;
build(l, mid, rt*2);
build(mid + 1, r, rt*2 + 1);
sum[rt] = sum[rt*2] + sum[rt*2 + 1];
}
三、线段树的维护：区间修改，单点修改，具体是啥后面在题里叙述
如何进行区间统计？
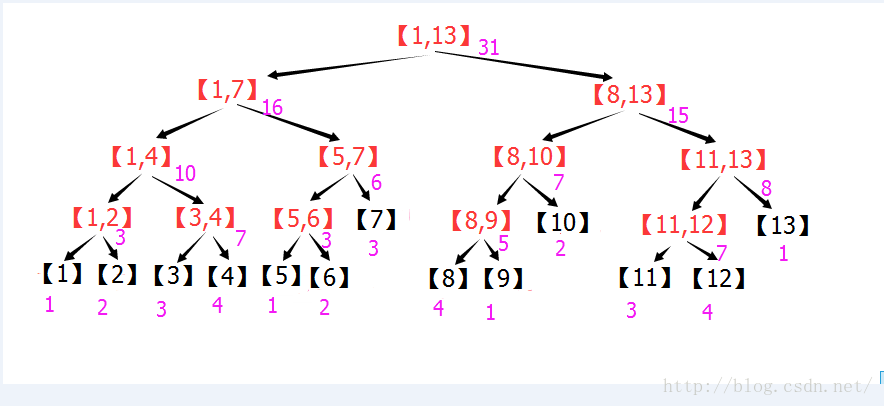
假设这13个数为1,2,3,4,1,2,3,4,1,2,3,4,1. 在区间之后标上该区间的数字之和：
如何进行点修改？
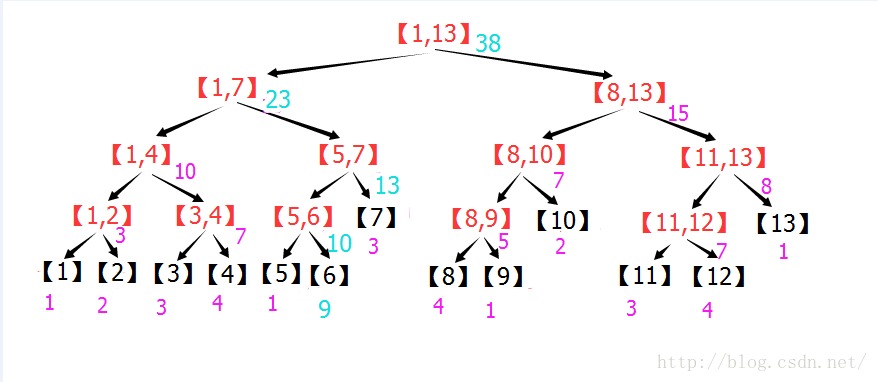
假设把A[6]+=7 ,看看哪些区间需要修改？[6],[5,6],[5,7],[1,7],[1,13]这些区间全部都需要+7.其余所有区间都不用动。
于是，这颗线段树中，点修改最多修改5个线段树元素（每层一个）。
下图中，修改后的元素用蓝色表示。
四、线段树的查询：
long long int query(int l, int r, int L, int R, int rt)//查询
{
if(L <= l && R >= r) return **区间维护的信息**;
int mid = (l + r) / 2;
if(L <= mid)
{
**代码**
}
if(R > mid)//这里不能加等于要不会炸
{
**代码**
}
return ans;
}
五、习题练习：
单点修改：数组计算机
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#define N 100005
long long int sum[N * 4], a[N];
void build(int l, int r, int rt)//建树
{
if(l == r)
{
sum[rt] = a[l];
return ;
}
int mid = (l + r) / 2;
build(l, mid, rt*2);
build(mid + 1, r, rt*2 + 1);
sum[rt] = sum[rt*2] + sum[rt*2 + 1];
}
void modify(int l, int r, int p, long long int v, int rt)//单点修改
{
if(l == r)
{
sum[rt] += v;
return ;
}
int mid = (l + r) / 2;
if(p > mid)
{
modify(mid + 1, r, p, v, rt*2 + 1);
}
else
{
modify(l, mid, p, v, rt*2);
}
sum[rt] = sum[rt*2] + sum[rt*2 + 1];
}
long long int query(int l, int r, int L, int R, int rt)//查询
{
if(L <= l && R >= r)
{
return sum[rt];
}
long long int ans = 0;
int mid = (l + r) / 2;
if(L <= mid)
{
ans += query(l, mid, L, R, rt*2);
}
if(R > mid)//这里不能加等于要不会炸
{
ans += query(mid + 1, r, L, R, rt*2 + 1);
}
return ans;
}
int main()
{
int n, m, i, q, T = 20;
while(~scanf("%d", &n) && T--)
{
memset(sum , 0, sizeof(sum));
memset(a, 0, sizeof(a));
for(i = 1;i <= n;i ++)
{
scanf("%lld", &a[i]);
}
build(1, n, 1);
scanf("%d", &m);
while(m--)
{
int p, l, r;
long long int v;
scanf("%d", &q);
if(q == 1)
{
scanf("%d %lld", &p, &v);
modify(1, n, p, v, 1);
}
else if (q == 2)
{
scanf("%d%d", &l, &r);
printf("%lld
", query(1, n, l, r, 1));
}
}
}
return 0;
}
区间修改：
lazy的思想：
Lazy：正常来说，区间改值，当更改某个区间的值的时候，子区间也该跟着更改，这样容易TLE。
Lazy思想就是更新到某个区间的时候，就先给这个区间打上标记，标记内容是需要更新的值，并把子区间的值改为子区间对应的值，清除该区间的lazy标记；然后return，不去更新子区间。当下一次更新或查询等需要访问该区间的子区间的时候再把该区间的lazy和其他信息送回子区间。
举个简单粗暴的例子：
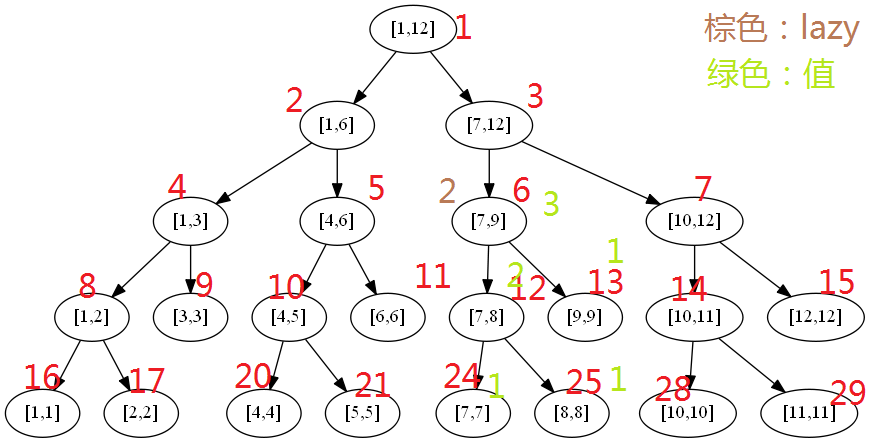
对应下面的那个图，假如目的是求和，现在要给[1,6] 的值都加2，那么我们从[1,12]->[1,6]，然后[1,6]的sum值加上区间长度[ (6-1+1)*2 ]，再把[1,6]的add[i]设置为2，就不再往下更新了【这里极大提高效率】。下一次更新/查询[1,6]的子区间时，我们将[1,6]原存的add值下传给[1,6]的两个直接子区间，再往下更新。假设在这种情况下，我们再更新[1,6]加3，则[1,6]的add值为2+3=5，然后我们查询[1,3]，则从上往下经过[1,6]时把[1,6]的add值给了子区间[1,3]和[4,6]，同时把sum[子区间]跟着子区间长度和add[父结点]改动，清除add[父节点]。【如果是查询间接子区间，则连续传递add值，也就是连续pushDown】
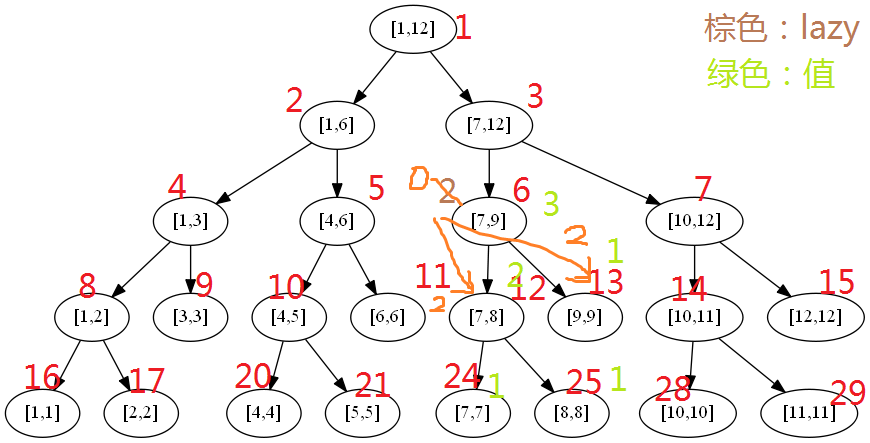
详细例子：假设update()是区间改值，query()是求和，所有叶子区间的和都为1，则[7,8]和[7,9]在build()的时候就附上了值（图中绿色字体）。假设此时我们更新[7,9]的值，改为2，则线段树从[1,12]->[7,12]->[7,9]，然后把[7,9]打上值为2的标记，求和（求和直接用区间长度*此时更新的值），然后不去更新[7,8]和[9,9]了，他们值仍然是2和1，lazy值为0。
然后我们查询[7,8]，当遍历经过[7,9]时
然后我们查询[7,8]，当遍历经过[7,9]时
if(add[i]) pushdown(i);
成立，把[7,9]的lazy标记2传给子区间[7,8]和[9,9],分别求这2个子区间的和，把[7,9]的lazy标记去掉，然后继续遍历，到[7,8]的时候直接返回答案。
C - A Simple Problem with Integers
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#define lt n<<1
#define rt n<<1|1
using namespace std;
typedef long long ll;
const int N = 1e6+5;
const int inf = 0x3f3f3f3f;
struct node
{
int ltree, rtree;
ll sum, lazy;
}tree[4*N];
int n, q, a[N];
void pushdown(int n)
{
tree[lt].sum += tree[n].lazy * (tree[lt].rtree - tree[lt].ltree + 1);
tree[rt].sum += tree[n].lazy * (tree[rt].rtree - tree[rt].ltree + 1);
tree[lt].lazy += tree[n].lazy, tree[rt].lazy += tree[n].lazy;
tree[n].lazy = 0;
}
void build(int l , int r, int n)
{
tree[n].ltree = l, tree[n].rtree = r;
tree[n].lazy = 0;
if(l == r)
{
tree[n].sum = a[l];
return ;
}
int mid = (l + r)>>1;
build(l, mid, lt);
build(mid+1, r, rt);
tree[n].sum = tree[lt].sum + tree[rt].sum;
}
ll query(int l, int r, int n)
{
int L = tree[n].ltree, R = tree[n].rtree;
if(tree[n].lazy) pushdown(n);
if(l <= L && r >= R) return tree[n].sum;
int mid = (L + R)>>1;
if(r <= mid) return query(l, r, lt);
else if(l > mid) return query(l, r, rt);
else return query(l, mid, lt) + query(mid+1, r, rt);
}
void uptade(int l, int r, int n, int num)
{
int L = tree[n].ltree, R = tree[n].rtree;
if(L == l && R == r)
{
// cout << l << r << endl;
tree[n].sum += (R - L + 1)*num;
tree[n].lazy += num;
return ;
}
if(tree[n].lazy) pushdown(n);
int mid = (L + R)>>1;
if(mid >= r) uptade(l, r, lt, num);
else if(mid < l) uptade(l, r, rt, num);
else
{
uptade(l, mid, lt, num);
uptade(mid+1, r, rt, num);
}
tree[n].sum = tree[lt].sum + tree[rt].sum;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> q;
for(int i = 1; i <= n; i++) cin >> a[i];
build(1, n, 1);
char c;
while(q--)
{
cin >> c;
if(c == 'Q')
{
int a, b;
cin >> a >> b;
cout << query(a, b, 1) << endl;
}
else
{
int a, b, c;
cin >> a >> b >> c;
uptade(a, b, 1, c);
}
}
return 0;
}
关于lazy 先乘后加的问题： 此时标记下传函数需要做些更改。
但这里涉及一个加法和乘法的顺序问题，因为axb+c和(a+c)xb（即先加再乘与先乘再加）是不一样的 分开看一下：
假设当前节点c，要将标记下传至x。 记加法标记add，乘法标记mul，值val。 记更改后的标记为add’和mul’
1.先乘后加 有方程：
(x.valx.mul+x.add)c.mul+c.add=x.valx.mul’+x.add’
不难解出：
x.mul’=x.mulc.mul
x.add’=x.add*c.mul+c.add
好像还可以，继续
2.先加后乘 有方程：
[(x.val+x.add)*x.mul+c.add]*c.mul=(x.val+x.add’)x.mul’
不难解出：
x.add’=(x.add+c.add)/c.mul
x.mul’=x.mulc.mul
注意 出现了除法！
我们知道，
除法不仅会影响答案的精度，有时还会出各种奇奇怪怪的问题 所以果断放弃后者，选择先乘后加。
这道题所囊括的思想是：对于多重标记的操作，先规定操作，再推倒关系。
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#define lt k<<1
#define rt k<<1|1
#define lson l, mid, lt
#define rson mid+1, r, rt
using namespace std;
const int maxn = 100005;
const int N = 10007;
struct node
{
int l,r;
int lazy1,lazy2,lazy3;//分别表示加号，乘号，等号标记
}t[maxn<<2];
int n;
void build(int l, int r, int k)
{
t[k].l = l;
t[k].r = r;
t[k].lazy1 = 0;
t[k].lazy2 = 1;
t[k].lazy3 = -1;
if(l == r)
{
t[k].lazy3 = 0;//最底层等号赋值为0
return;
};
int mid = (l+r)>>1;
build(lson);
build(rson);
}
void pushdown(int k)
{
if(t[k].l == t[k].r) return;
if(t[k].lazy3 != -1)//处理等号
{
t[lt].lazy3 = t[rt].lazy3 = t[k].lazy3;//更新子区间等号标记
t[lt].lazy2 = t[rt].lazy2 = 1;//清空子区间加乘标记
t[lt].lazy1 = t[rt].lazy1 = 0;
t[k].lazy3 = -1;
return;
}
if(t[k].lazy2 != 1)//处理乘号
{
if(t[lt].lazy3 != -1) t[lt].lazy3 = (t[lt].lazy3*t[k].lazy2) % N;//如果子区间有等号标记，直接修改等号标记
else//否则清空该子区间标记，进行子区间标记
{
pushdown(lt);
t[lt].lazy2 = (t[lt].lazy2*t[k].lazy2)%N;
}
if(t[rt].lazy3 != -1) t[rt].lazy3=(t[rt].lazy3*t[k].lazy2) % N;//同理
else
{
pushdown(rt);
t[rt].lazy2=(t[rt].lazy2*t[k].lazy2)%N;
}
t[k].lazy2=1;//清空乘法标记
}
if(t[k].lazy1!=0)//处理加号标记
{
if(t[lt].lazy3 != -1) t[lt].lazy3=(t[lt].lazy3+t[k].lazy1)%N;
else
{
pushdown(lt);
t[lt].lazy1 = (t[lt].lazy1+t[k].lazy1)%N;
}
if(t[rt].lazy3 != -1) t[rt].lazy3=(t[rt].lazy3+t[k].lazy1)%N;
else
{
pushdown(rt);
t[rt].lazy1=(t[rt].lazy1+t[k].lazy1)%N;
}
t[k].lazy1=0;//记得清空
}
}
void update(int l, int r, int num, int d, int k)
{
if(t[k].l == l && t[k].r == r)
{
if(d == 1)
{
if(t[k].lazy3!=-1) t[k].lazy3=(t[k].lazy3+num)%N;//如果有等号标记，就直接修改等号标记
else
{
pushdown(k);//否则清空该区间，进行标记
t[k].lazy1 = (t[k].lazy1+num)%N;
}
}
else if(d == 2)//同理
{
if(t[k].lazy3 != -1) t[k].lazy3=(t[k].lazy3*num)%N;
else
{
pushdown(k);
t[k].lazy2 = (t[k].lazy2*num) % N;
}
}
else
{
t[k].lazy3=num%N;
t[k].lazy1=0;
t[k].lazy2=1;
}
return;
}
pushdown(k);//向下更新
int mid = (t[k].l+t[k].r)>>1;
if(r <= mid) update(l,r,num,d,lt);
else if(l>mid) update(l,r,num,d,rt);
else
{
update(l,mid,num,d,lt);
update(mid+1,r,num,d,rt);
}
}
int query(int l,int r,int p,int k)
{
if(t[k].l>=l&&t[k].r<=r&&t[k].lazy3!=-1)//查到是查询区间的子区间且一段全为相同的数
{
int temp = 1;
for(int i = 1;i <= p;i++) temp = (temp*t[k].lazy3)%N;
return ((t[k].r-t[k].l+1)*temp)%N;//注意要乘上长度
}
pushdown(k);
int mid = (t[k].l + t[k].r)>>1;
if(r <= mid) return query(l,r,p,lt)%N;
else if(l > mid) return query(l,r,p,rt)%N;
else return (query(l,mid,p,lt)+query(mid+1,r,p,rt))%N;
}
int main()
{
int m;
while(~scanf("%d%d",&n,&m))
{
if(!n && !m) break;
build(1,n,1);
for(int i = 0;i < m;i++)
{
int d,x,y,c;
scanf("%d%d%d%d",&d, &x, &y, &c);
if(d >= 1 && d <= 3) update(x,y,c,d,1);
else printf("%d
",query(x,y,c,1)%N);
}
}
return 0;
}
参考博客：说人话的线段树──懒人标记、线段树从零开始