算法初探

更新记录

【1】2020.05.21-00:36

1.完善dijkstra

【2】2020.05.21-11:25

1.完善dijkstra堆优化

【3】2020.06.11-17:43

1.更新内容

正文

铅制芝士（会一点点就行啦~）

• 动态规划
• 贪心
• 链式前向星
• 堆

持续更新中...

最短路算法是图论算法必学算法之一
那么既然它这么重要，就更需要我们深入了解，熟练掌握
（默认图为连通图）

dijkstra算法

有点贪心动规的意思

• 我们可以发现，起点到任何一个点的最短路都要经过至少一个的中转点（起点s也算一个中转点）
• 那么我们发现，如果想求出这个点的最短路，那么必定要求出它中转点的最短路
• • 首先dijkstra算法不能处理负边权，所以我们在使用时默认图无负边权
• • 所以1-其中一个中转点的最短路，一定小于等于1-终点的最短路
• • 当小于时，中转点比其先确定最短路
• • 当等于时，谁先处理都是一样的结果
• 那么依此类推，最后终将推到一个最最最简单的问题：两点间的最短路

这个问题只要你会存图就会做
（很像动态规划对不对）

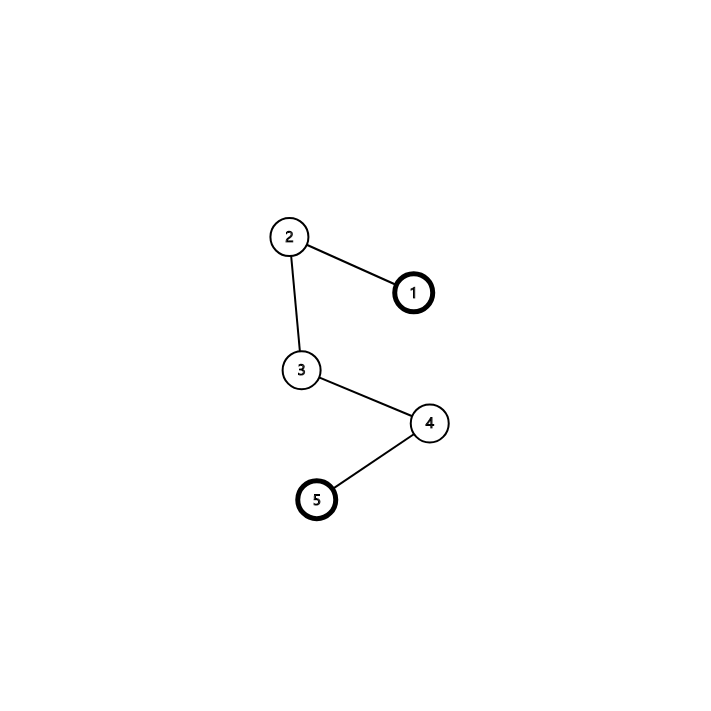
^RT，我们要求出1-5的最短路径

就必须求出起点到中转点的最短路径，中转点为4

想求出1-4的最短路径，就先去求1-3的最短路径

同理求1-2的最短路

而1-2的最短路就是其连接的边的权值

算法思路：

定义变量（链式前向星的那堆变量就不再重复写了）：
dis[i]：表示从起点到i的最短距离
f[i]：记录这条边有没有被确定过最短路
s表示起点

初始化：dis[i]=∞;dis[s]=0

遍历每一个点

• 对于每一个点a，找到一个dis[b]最小的顶点b
• b被确定过最短路
• 遍历所有以b为起点的边，更新它们的dis
  算法结束

#include<iostream>
using namespace std;
#define NUM 500050
#define INF 2147483647
struct Edge{
	int na,np,w;
}e[NUM];
int head[NUM],dis[NUM],num,n,m,s,u,v,w,minn;
bool f[NUM];
inline void add(int f,int t,int w){
	e[++num].na=head[f];
	e[num].np=t,e[num].w=w;
	head[f]=num;
}
int main(){
	cin>>n>>m>>s;
	for(int i=0;i<m;i++){
		cin>>u>>v>>w;
		add(u,v,w);
	}
//初始化
	for(int i=1;i<=n;i++) dis[i]=INF;
	dis[s]=0;
//遍历每一个点
	for(int i=1;i<=n;i++){
//对于每一个点a，找到一个dis[b]最小的顶点b
		minn=-1;
		for(int o=1;o<=n;o++)
			if(f[o]==0&&(dis[minn]>dis[o]||minn==-1)) minn=o;
//b被确定过最短路
		f[minn]=1;
//遍历所有以b为起点的边，更新它们的dis
		for(int o=head[minn];o!=0;o=e[o].na)
			if(!f[e[o].np])
				dis[e[o].np]=min(dis[e[o].np],dis[minn]+e[o].w);
	}
//算法结束，输出s到各点的最短距离
	for(int i=1;i<=n;i++) cout<<dis[i]<<" ";
}

dijkstra堆优化

我们可以发现，对于原来的dijkstra算法，每次查找最小值时间复杂度都为O(n)
这显然很慢啊！！！

那么有什么算法可以在常数时间内求出最小值呢？
当然是（线段树）堆啦！

建立一个小根堆，即可迅速求出所有数据的最小值
整个算法的复杂度也降低了不少

我们发现，对于每次扫描，会有一些数据已经确定过最小值，再次进行扫描会浪费时间
所以我们要使用队列来实现

最终结论：用优先队列+二元组实现
明白了这个之后，这道题对你来说+岩浆=黑曜石

#include<cstdio>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
#define ll int
#define NUM 500050
#define INF 2147483647
struct Edge{
	int na,np,w;
}e[NUM];
ll head[NUM],dis[NUM],num,n,m,s,u,v,w,minn,bf,i;
bool f[NUM];
priority_queue<pair<ll,ll>,vector<pair<ll,ll> >,greater<pair<ll,ll> > >q;
inline void add(int f,int t,int w){
	e[++num].na=head[f];
	e[num].np=t,e[num].w=w;
	head[f]=num;
}
inline int read() {
    int X=0,W=1; char c=getchar();
    while (c<'0'||c>'9') { if (c=='-') W=-1; c=getchar(); }
    while (c>='0'&&c<='9') X=(X<<3)+(X<<1)+c-'0',c=getchar();
    return X*W;
}
int main(){
	n=read();m=read();s=read();
	for(i=0;i<m;++i){
		u=read();v=read();w=read();
		add(u,v,w);
	}
	for(int i=1;i<=n;++i) dis[i]=INF;
	dis[s]=0;
//以上全部为初始化
	q.push(make_pair(0,s));
//将起点压进队列
	while(q.size()){
//如果队列里还有元素
		bf=q.top().second;q.pop();
//bf为当前次遍历的起点，保存后将这个元素弹出
		if(f[bf]) continue;
//搜过了就不搜了
		f[bf]=1;
//没搜过就标记一下
		for(int i=head[bf];i;i=e[i].na){
//同样的遍历
			if(dis[bf]+e[i].w<dis[e[i].np]){
//找到了更短的路径
				dis[e[i].np]=dis[bf]+e[i].w;
//更新
				q.push(make_pair(dis[e[i].np],e[i].np));
//既然有更优解那就将这个点压进队列，用来更新其他点
			}
		}
	}
	for(int i=1;i<=n;++i) printf("%d ",dis[i]);
//out
}

那么至于为什么make_pair的参数是最短距离，边的终点呢？

为什么不反过来存或存其他的参数呢

因为这是个自动排序的优先队列啊
因为二元组自带排序规则啊