题目
翻译
新冠肺炎时代,平时也不上网课,也懒得背单词,就翻译个 CF 题面装装还在学英语的样子 ……
(以上那句和这句题面里没有)
题目名:狐狸多边形
描述
狐狸塞尔设计了一个叫做「多边形」的解谜游戏!这个游戏与 (n) 条边的正多边形的三角剖分有关。目标是根据一些奇特的规则从一个三角剖分转换到另一个三角剖分。
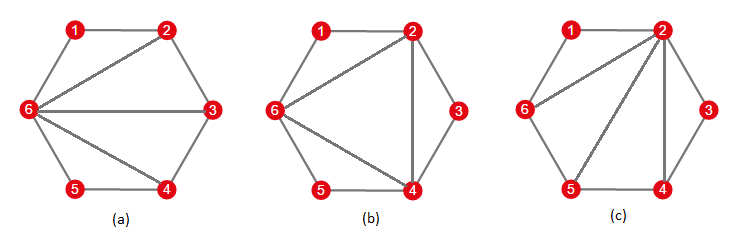
正多边形的 三角剖分 定义为一个包含 (n-3) 条对角线的集合,满足没有两条对角线在多边形内部(不含边界)相交。
例如,游戏的初始状态是上图中的 (a) ,你的目标是上图中的 (c) 。每一步你可以在多边形中选一条对角线(不能选多边形的边),并 翻转 这条对角线。
如果你准备翻转对角线 (a-b) ,(a-b) 总是两个三角形的公共边,设这两个三角形是 (a-b-c) 和 (a-b-d) 。操作的结果是,对角线 (a-b) 被对角线 (c-d) 取代。可以轻易地证明,翻转操作后的对角线集合仍然是多边形的一个三角剖分。
所以对于上图中的情况,你可以先翻转对角线 (6-3) ,它会被对角线 (2-4) 取代。然后翻转对角线 (6-4) ,就能得到图 (c) 的结果。
塞尔刚刚证明了对于任意一种起始和目标状态,这个游戏都有解。她希望你在不超过 (20000) 步内解决任意一个满足 (nleq 1000) 的谜题。
输入
第一行包含一个整数 (n(4leq nleq 1000)) ,正多边形的边的数量。
紧跟着包含两组 ((n-3)) 行,分别描述初始三角剖分和目标三角剖分。
每一个三角剖分的描述由 ((n-3)) 行组成。每一行包含两个整数 (a_i) 和 (b_i(1leq a_i,b_ileq n)) ,描述一条对角线 (a_i-b_i) 。
保证初始和目标三角剖分都是正确的(即两个三角剖分中都没有两条边在多边形内部相交)。
输出
首先,输出整数 (k(0leq kleq 20000)) :步数。
然后输出 (k) 行,每一行包含两个整数 (a_i) 和 (b_i) :第 (i) 步你将翻转的对角线的两个端点。你可以以任意顺序输出 (a_i) 和 (b_i) 。
如果有多种可能的解,请任意输出一种。
分析
我用的是题解评论区的做法,题解的做法实在太麻烦了(并且一般人都想不到吧 …… )。评论区的做法思路清晰,解法自然,码量适中。
显然这个操作是可逆的。即如果知道了一种从 (A) 到 (B) 的方法,那么倒着做一遍就可以从 (B) 到 (A) 。那么找一个特殊状态 (S) ,分别算出从初始状态和目标状态到 (S) 的方案,把前者和后者的逆序拼接起来就是最终方案。方便起见,把 (S) 定为由从 (1) 出发的 (n-3) 条对角线组成的集合。现在的问题变成了如何从一个任意状态变换到这种状态。
方案还是比较好构造的。考虑从 (1) 号点发出的边(包括所有从 (1) 发出的对角线和 (1-2) 、 (1-(n-1)) 这两条边,因此至少存在两条)中相邻的两条 (1-a) 和 (1-b) ,且 (a) 和 (b) 不是连续的两个点(如果不存在说明已经是状态 (S) 了),那么一定存在 (a-b) 这条边,否则不是一个三角剖分。翻转 (a-b) 这条边,得到 (1-c) ,其中 (c) 是 (a) 和 (b) 之间的一个特定的点。这样,从 (1) 出发的对角线就增加了一条。综上所述,任意一种状态最多操作 (n-3) 次就能到达 (S) ,因此这样操作的答案上界是 (2n-6) ,可以通过。具体实现细节详见代码。
代码
注意计算目标状态到 (S) 时应该记录的是变换后得到的边而不是变换前的边。
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <set>
using namespace std;
namespace zyt
{
template<typename T>
inline bool read(T &x)
{
char c;
bool f = false;
x = 0;
do
c = getchar();
while (c != EOF && c != '-' && !isdigit(c));
if (c == EOF)
return false;
if (c == '-')
f = true, c = getchar();
do
x = x * 10 + c - '0', c = getchar();
while (isdigit(c));
if (f)
x = -x;
return true;
}
template<typename T>
inline void write(T x)
{
static char buf[20];
char *pos = buf;
if (x < 0)
putchar('-'), x = -x;
do
*pos++ = x % 10 + '0';
while (x /= 10);
while (pos > buf)
putchar(*--pos);
}
const int N = 1e3 + 10;
typedef pair<int, int> pii;
int n, anscnt, buf[N];
set<int> s[N];
pii ans[N << 1];
void solve(const int l, const int r, const bool flag)
{
if (r == l + 1)
return;
int tmp;
s[1].insert(tmp = *--s[l].lower_bound(r)), s[tmp].insert(1);
s[l].erase(r), s[r].erase(l);
ans[anscnt++] = (flag ? pii(l, r) : pii(1, tmp));
solve(l, tmp, flag), solve(tmp, r, flag);
}
int work()
{
read(n);
for (int i = 2; i < n; i++)
s[i].insert(i + 1), s[i].insert(i - 1);
s[1].insert(2), s[1].insert(n);
s[n].insert(1), s[n].insert(n - 1);
for (int i = 1; i <= n - 3; i++)
{
int a, b;
read(a), read(b);
s[a].insert(b), s[b].insert(a);
}
int cnt = 0;
for (set<int>::iterator it = s[1].begin(); it != s[1].end(); it++)
buf[cnt++] = *it;
for (int i = 1; i < cnt; i++)
solve(buf[i - 1], buf[i], true);
int tmp = anscnt;
for (int i = 1; i <= n; i++)
s[i].clear();
for (int i = 2; i < n; i++)
s[i].insert(i + 1), s[i].insert(i - 1);
s[1].insert(2), s[1].insert(n);
s[n].insert(1), s[n].insert(n - 1);
for (int i = 1; i <= n - 3; i++)
{
int a, b;
read(a), read(b);
s[a].insert(b), s[b].insert(a);
}
cnt = 0;
for (set<int>::iterator it = s[1].begin(); it != s[1].end(); it++)
buf[cnt++] = *it;
for (int i = 1; i < cnt; i++)
solve(buf[i - 1], buf[i], false);
reverse(ans + tmp, ans + anscnt);
write(anscnt), putchar('
');
for (int i = 0; i < anscnt; i++)
write(ans[i].first), putchar(' '), write(ans[i].second), putchar('
');
return 0;
}
}
int main()
{
return zyt::work();
}