乘风破浪：LeetCode真题_015_3Sum

乘风破浪：LeetCode真题_015_3Sum

一、前言

    关于集合的操作，也是编程最容易考试的问题，比如求集和中的3个元素使得它们的和为0，并且要求不重复出现，这样的问题该怎么样解决呢？

二、3Sum

2.1 问题

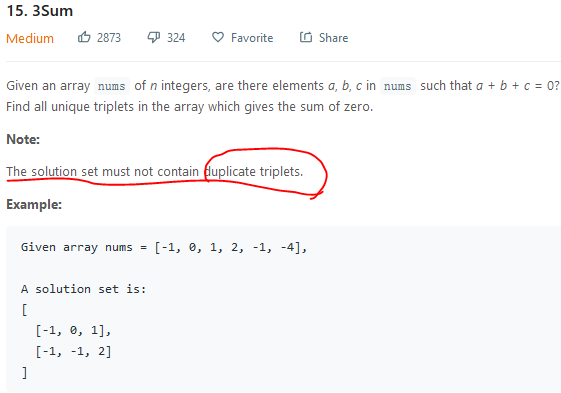
2.2 分析与解决

    遇到这样的问题，我们更应该仔细想想如果使用暴力法的时间效率，可以发现是O(n~3)的时间复杂度，并且会出现重复过的，需要去除重复，这是非常让人难以忍受的，并且我们知道随着集合的增大，这样的代价非常的大。那么我们如何进行优化呢，这里就要仔细的想想如果我们在第一个循环中确定了前面的元素，后面的循环不能再使用这些元素，并且在后面的操作中找到两个数，这样两个数的和正好等于负的当前的数，这样和就为零了。但是我们这样做还是会有很多的问题，比如无法去除重复的情况，因此，如果我们实现对数组进行排序，得到从小到大的数组，然后在进行上面的操作，如果遇到相邻的两个数是相等的，我们就跳过去，这样就完美的解决问题了。

       比如下面的代码：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> out = new ArrayList<>();
        if (nums == null || nums.length < 3) {
            return out;
        }
        Arrays.sort(nums);
        
        for (int i = 0; i < nums.length-2; i++) {
            //NO duplicates allowed!
            if (i > 0 && nums[i] == nums[i-1]) {
                continue;
            }
            int complement = -1*nums[i];
            int j = i+1;
            int k = nums.length - 1;
            //no way for a triplet to be equal to 0.
            if (nums[j] > complement) {
                continue;
            }
            
            while(j < k) {
                int sum = nums[j] + nums[k];
                if(sum == complement) {
                    out.add(Arrays.asList(new Integer[]{nums[i],nums[j],nums[k]}));
                    j++;
                    k--;
                    while(j < k && nums[j] == nums[j-1]) {
                        j++;
                    }
                    while(j < k && nums[k] == nums[k+1]) {
                        k--;
                    }
                } else if (sum < complement) {
                    j++;
                } else {
                    k--;
                }
            }
        }
        return out;
    }
}

      这样的时间复杂度，排序以及后面算法一共为O(n~2)。

         同时还可以做一些改进，将下面代码进行优化，

                } else if (sum < complement) {
                    j++;
                } else {
                    k--;
                }

      直接寻找到最适合的目标。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

public class Solution {
    /**
     * Note:
     * The solution set must not contain duplicate triplets.
     *
     * For example, given array S = {-1 0 1 2 -1 -4},
     * A solution set is:
     * (-1, 0, 1)
     * (-1, -1, 2)
     *
     * 题目大意：
     * 给定一个n个元素的数组，是否存在a，b，c三个元素，使用得a+b+c=0，找出所有符合这个条件的三元组
     *
     * 注意：
     *   - 三元组中的元素必须是非递减的
     *   - 结果不能包含重复元素
     *
     * 解题思路：
     * 可以在 2sum问题 的基础上来解决3sum问题，假设3sum问题的目标是target。每次从数组中选出一个数k，
     * 从剩下的数中求目标等于target-k的2sum问题。这里需要注意的是有个小的trick：当我们从数组中选出
     * 第i数时，我们只需要求数值中从第i+1个到最后一个范围内字数组的2sum问题。
     *
     * 我们以选第一个和第二个举例，假设数组为A[],总共有n个元素A1，A2....An。很显然，当选出A1时，
     * 我们在子数组[A2~An]中求目标位target-A1的2sum问题，我们要证明的是当选出A2时，我们只需要在
     * 子数组[A3~An]中计算目标位target-A2的2sum问题，而不是在子数组[A1,A3~An]中，证明如下：
     * 假设在子数组[A1,A3~An]目标位target-A2的2sum问题中，存在A1 + m = target-A2（m为A3~An中
     * 的某个数），即A2 + m = target-A1，这刚好是“对于子数组[A3~An],目标位target-A1的2sum问题”
     * 的一个解。即我们相当于对满足3sum的三个数A1+A2+m = target重复计算了。因此为了避免重复计算，
     * 在子数组[A1，A3~An]中，可以把A1去掉，再来计算目标是target-A2的2sum问题。
     *
     * 对于本题要求的求最接近解，只需要保存当前解以及当前解和目标的距离，如果新的解更接近，则更新解。
     * 算法复杂度为O（n^2）;
     */
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new LinkedList<>();

        if (nums != null && nums.length > 2) {
            // 先对数组进行排序
            Arrays.sort(nums);
            // i表示假设取第i个数作为结果
            for (int i = 0; i < nums.length - 2; ) {
                // 第二个数可能的起始位置
                int j = i + 1;
                // 第三个数可能是结束位置
                int k = nums.length - 1;

                while (j < k) {
                    // 如果找到满足条件的解
                    if (nums[j] + nums[k] == -nums[i]) {
                        // 将结果添加到结果含集中
                        List<Integer> list = new ArrayList<>(3);
                        list.add(nums[i]);
                        list.add(nums[j]);
                        list.add(nums[k]);
                        result.add(list);

                        // 移动到下一个位置，找下一组解
                        k--;
                        j++;

                        // 从左向右找第一个与之前处理的数不同的数的下标
                        while (j < k && nums[j] == nums[j - 1]) {
                            j++;
                        }
                        // 从右向左找第一个与之前处理的数不同的数的下标
                        while (j < k && nums[k] == nums[k + 1]) {
                            k--;
                        }
                    }
                    // 和大于0
                    else if (nums[j] + nums[k] > -nums[i]) {
                        k--;
                        // 从右向左找第一个与之前处理的数不同的数的下标
                        while (j < k && nums[k] == nums[k + 1]) {
                            k--;
                        }
                    }
                    // 和小于0
                    else {
                        j++;
                        // 从左向右找第一个与之前处理的数不同的数的下标
                        while (j < k && nums[j] == nums[j - 1]) {
                            j++;
                        }
                    }
                }

                // 指向下一个要处理的数
                i++;
                // 从左向右找第一个与之前处理的数不同的数的下标
                while (i < nums.length - 2 && nums[i] == nums[i - 1]) {
                    i++;
                }
            }
        }

        return result;
    }
}

 

三、总结

    看到了这样的问题，我们将三个数的求和转换成了两个数的求和，这是非常具有开创性的意见的，同时对于更多的数，我们也可以转换成三个数，最后转成两个数的求和算法来计算，另外对于一些优化问题，也是值得我们去思考的。