2019 年百度之星·程序设计大赛

题目链接

1001 Polynomial （基础数学）

Accepts: 2234

Submissions: 5283

Time Limit: 2000/1000 MS (Java/Others)

Memory Limit: 32768/32768 K (Java/Others)

Problem Description

度度熊最近学习了多项式和极限的概念。 现在他有两个多项式 f(x) 和 g(x)，他想知道当 x 趋近无限大的时候，f(x)/g(x) 收敛于多少。

Input

第一行一个整数 T (1≤T≤100) 表示数据组数。 对于每组数据，第一行一个整数 n (1≤n≤1,000)，n−1 表示多项式 f 和 g 可能的最高项的次数（最高项系数不一定非0）。 接下来一行 n 个数表示多项式 f，第 i 个整数 fi (0≤fi≤1,000,000) 表示次数为 i−1 次的项的系数。 接下来一行 n 个数表示多项式 g，第 i 个整数 gi (0≤gi≤1,000,000)表示次数为 i−1 次的项的系数。 数据保证多项式 f 和 g 的系数中至少有一项非0。

Output

对于每组数据，输出一个最简分数 a/b（a 和 b 的最大公约数为1）表示答案。 如果不收敛，输出 1/0。

Sample Input

3
2
0 2
1 0
2
1 0
0 2
3
2 4 0
1 2 0

Sample Output

1/0
0/1
2/1

样例描述
这些多项式分别为
f(x)=2xf(x) = 2xf(x)=2x
g(x)=1g(x) = 1g(x)=1
f(x)=1f(x) = 1f(x)=1
g(x)=2xg(x) = 2xg(x)=2x
f(x)=4x+2f(x) = 4x + 2f(x)=4x+2
g(x)=2x+1g(x) = 2x + 1g(x)=2x+1

题意分析：

给出两个多项式各项的系数，求f(x)/g(x)趋近多少。

解题思路：

当两者的最高项都不为0时，趋近与两者之比；

当f(x)最高项为0时趋近0，即0/1，

当g(x)最高项为0时趋近1，即1/0。

此最高项是两者中次数大的项， 注意化简为最简分数。

#include <stdio.h>
#include <algorithm>
#define N 1020
using namespace std;
int a[N], b[N];
int main() {
	int t, n;
	scanf("%d", &t);
	while(t--)
	{
		scanf("%d", &n);
		for(int i=0; i<n; i++)
			scanf("%d", &a[i]);
		for(int i=0; i<n; i++)
			scanf("%d", &b[i]);
		for(int i=n-1; i>=0; i--)
		{
			if(a[i]==0 && b[i]==0)
				continue;
			if(a[i]==0)
			{
				printf("0/1
");
				break;
			}
			
			else if(b[i]==0) {
				printf("1/0
");
				break;
			}	
			else 
			{
				int c=__gcd(a[i], b[i]);
				printf("%d/%d
", a[i]/c, b[i]/c);
				break;
			}
		}
	}
	return 0;
}

1002 Game （贪心模拟）

Accepts: 572

Submissions: 6218

Time Limit: 2000/1000 MS (Java/Others)

Memory Limit: 32768/32768 K (Java/Others)

Problem Description

度度熊在玩一个好玩的游戏。 游戏的主人公站在一根数轴上，他可以在数轴上任意移动，对于每次移动，他可以选择往左或往右走一格或两格。 现在他要依次完成 n 个任务，对于任务 i，只要他处于区间 [ai,bi]上，就算完成了任务。 度度熊想知道，为了完成所有的任务，最少需要移动多少次？ 度度熊可以任意选择初始位置。

Input

第一行一个整数 T (1≤T≤10)表示数据组数。 对于每组数据，第一行一个整数 n (1≤n≤1000) 表示任务数。 接下来 n 行，第 iii 行两个整数 ai,bi (1≤ai≤bi≤1000000) 表示任务对应的区间。

Output

对于每组数据，一行一个整数表示答案。

Sample Input

1
2
1 10
20 30

Sample Output

5

样例描述
选取10为起点，经过的轨迹为10-12-14-16-18-20。

题意分析：

给出n个区间，初始位置可选，依次到达相应的区间，每次可以移动一格或两格，求最小步数。

解题思路：

因为只要在这个区间中就可以完成任务，第一次的位置可选，所以初始位置可以选前几个任务的相交区间中，这样一次可以完成更多的任务， 此时若所以任务都完成即可结束，否则继续计算。

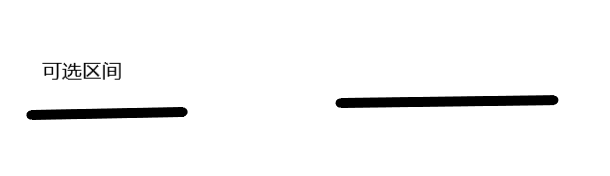
此时前面所有任务的相交区间是一个可选区间，也就是说初始位置可以选这个区间中的任意一个数，下一个任务不会和此区间重合，因为重合的区间会在前面计算在内，                                                                                                                                        很容易想到如果下一任务在区间右侧，应该选最靠右的点，                                                                                                            同理如果下一任务在区间左侧，应该选最靠左的点。

此时位置已经确定，在考虑任务时，在此区间内自然不用考虑，所以只看两种情况，用sum代表当前位置，两种情况为sum>b[i]和sum < a[i]。

在此有一个可移动步数，如果现在两步两步的移动可以到达箭头指向的地方，下一任务如果是第3个的左边区间，那么这样移动是对的，但如果是右边区间，那么之前移动的最后的2步应该改成1步，也就是说向右移动1步可以使贪心策略最佳，如果这个区间只有一个点，就不能移动。

上面考虑的是下一任务在sum左边的情况，在sum右边时同样可以推出来。

#include <stdio.h>
#include <algorithm>
#define N 1020
using namespace std;
int a[N], b[N];
int main() {
    int t, n, l, r, i;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        scanf("%d%d", &a ,&b);
        
        for(i=1; i<n; i++)
            scanf("%d%d", &a[i], &b[i]);
        l=a[0];r=b[0];
        for(i=1; i<n; i++) {                        //选相交区间
            if(max(l, a[i])>min(r, b[i]))
                break;
            l=max(l, a[i]);
            r=min(r, b[i]);
        }
        if(i==n)                                  //所有任务完成，结束
        {
            printf("0
");
            continue;
        }
        int ans=0, sum;
        
        if(b[i]<l) 
            sum=l;  
        else sum=r;
        int temp=0;
  
        for(; i<n-1; i++)                     //没有考虑最后一个，因为要用到 i+1 项任务
        {
            if(sum>b[i]) {
                if (temp==-1)                 //步数可以移动
                    sum--;
                ans+=(sum-b[i]+1)/2;           //更新步数
                if((sum-b[i])%2==1 && b[i]-a[i]>=1)      //判断区间只有一个点的情况
                    temp=-1;                       //更新可以移动的步数
                else temp=0;      
                sum=b[i];                        //更新位置
            }
            else if(sum < a[i]) {
                if (temp==1)
                    sum++;
                ans+=(a[i]-sum+1)/2;
 
                if((a[i]-sum)%2==1 && b[i]-a[i]>=1)
                    temp=1;
                else temp=0;
                sum=a[i];
            }
            else {
                if (sum==a[i] && temp==-1)
                    temp=0;
                else if (sum==b[i] && temp==1)
                    temp=0;
            }
        }
        //printf("!%d %d %d
", sum, ans, temp);
        if(sum>b[i]) {                    //考虑最后一个
            if (temp==-1)
                sum--;
            ans += (sum-b[i] + 1)/2;
        }
        else if(sum<a[i]) {
            if (temp==1)
                sum++;
            ans+=(a[i]-sum+1)/2;
        }
        
        printf("%d
",ans);
    }
    return 0;
}
/**
3
1 2
2 3
1 1
3
5 6
1 2
7 8
4
1 10
2 8
11 12
12 13

4 
4 4 
5 10 
3 5 
8 10 
*/
 

1005 Seq （找规律）

Accepts: 1283

Submissions: 3956

Time Limit: 2000/1000 MS (Java/Others)

Memory Limit: 32768/32768 K (Java/Others)

Problem Description

度度熊有一个递推式 其中a​1​​=1。现给出 n，需要求 an。

Input

第一行输入一个整数 T，代表 T (1≤T≤100000组数据。 接下 T 行，每行一个数字 n (1≤n≤10^12)。

Output

输出 T 行，每行一个整数表示答案。

Sample Input

5
1
2
3
4
5

Sample Output

1
1
0
3
0

题意分析：

给出n，求( a[1] * 1 + a[2] * 2 + …… + a[n-1]*(n-1) ) % n;

解题思路：

先打个表出来，依次代表n，n/6,  a[n]。

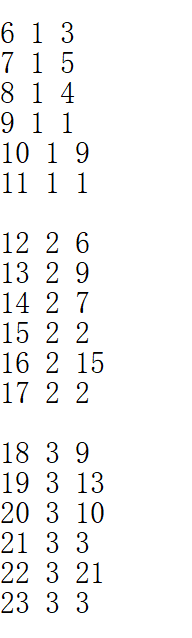
发现这个每6个是一轮，第一次打表的时候，也是没有发现规律的，最后才加上了中间的n/6。

第一个数是n/2；

第二个数是1+（n/6）* 4；

第三个数是1+（n/6）* 3；

第四个数是（n/6）；

第五个数是3+（n/6）*6；

第六个数是n/6。

只要求出对6取余是哪一个数，输出相应的公式即可。

#include <stdio.h>
int main()
{
	int T;
	long long n;
	scanf("%d", &T);
	while(T--)
	{
		scanf("%lld", &n);
		long long t=n/6;
		if(n%6==3 || n%6==5)
			printf("%lld
", t);
		else if(n%6==0)
			printf("%lld
", n/2);
		else if(n%6==1)
			printf("%lld
", 1+t*4);
		else if(n%6==2)
			printf("%lld
", 1+t*3);
		else if(n%6==4)
			printf("%lld
", 3+t*6);
	}
	return 0;
}