Plane-Sweep:
平面扫描是二维的几何问题产生的算法范式。它的想法是用一条直线去扫描并且对于遇到的第一个数据进行处理。我们用这个想法解决三个问题:构造一些点的凸包,对凸包进行三角剖分,检测直线的交叉点。
首先介绍了凸包。设S是平面中给定两个坐标值的一系列点的集合,S的凸包记作convS,是S的所有凸集中最小的一个。把点想象成板子上的钉子,然后用一个橡皮筋在外面的钉子周围绕一圈,放手之后橡皮筋自然会跟踪凸包的边界。为了构造凸包,我们用一条直线从左到右扫描平面,直线左边的顶点都是处理好的,直线右边的点是待处理的。我们按横坐标对点进行排序为x1,x2,...,xn;然后选择前三个点用逆时针的方式形成一个三角形为x1x2x3或者是x1x3x2;对于i = 4 to n,我们按照一下方式加入xi,过xi作两条直线,要求它们可以支持这个凸包(理解成夹住凸包),然后连接xi和对应的两个顶点,就可以了。这三步完成之后就形成了凸包,下面是一个例子:
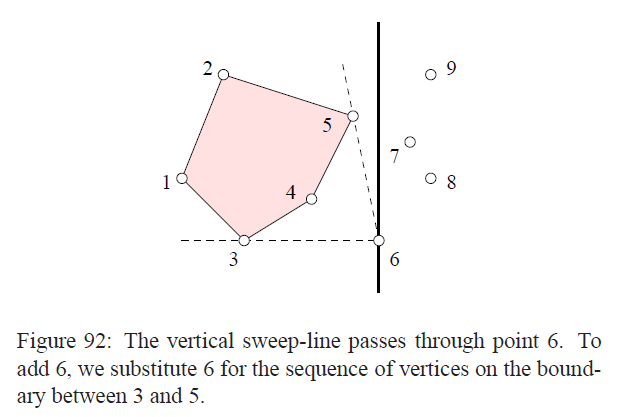
这个图展示的是加入6的这个点的过程,作了两条直线63和65,支撑了这个凸包,然后连接起来就形成了新的凸包。
然后介绍了定向,如何决定访问三个点的顺序是逆时针还是顺时针呢?其实只要结合行列式就可以了,因为可以通过行列式来计算面积,根据面积的正负来判断当前的方向。
接着介绍了寻找支撑线(支持线)的方法,重要的部分在于怎么样找到支撑的两个点,实际上我们要结合定向来寻找,我们发现对于要加入的点v来说,两个支撑的点是在和相邻的点形成的三角形的方向产生了不同,算法见下:


为了分析这个过程,我们用摊还的方法,插入一个点耗费2元,1元付add,另外一元付未来的delete,这样一来我们就可以覆盖所有的while,所以我们整个的操作是O(N)的。每次操作是常数级别的。
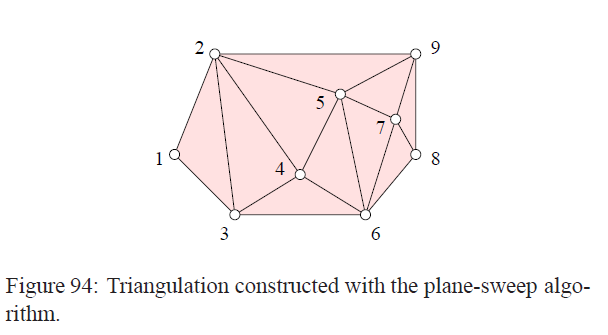
同样的平面扫描算法可以用来把一个凸包分解成若干三角形。同样的平面扫描算法可以将凸包分解成三角形。我们需要改变的是,点和边永远不会被删除,一个新的点连接到两个while循环期间检查的每个点。下图是一个之前那个构造凸包的图用来执行分解为三角形时的过程:
接着介绍线段交点的问题,假设没有三条线段交在一个点,我们先来判断两条线段何时相交。假设UV的顶点坐标为U(u1,u2)和V(v1,v2),PQ的顶点坐标为P(p1,p2)和Q(q1,q2),那么有下面函数来判断是否相交:
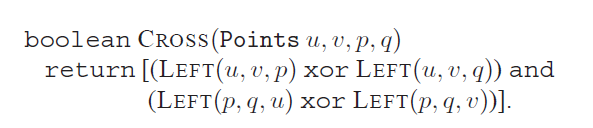
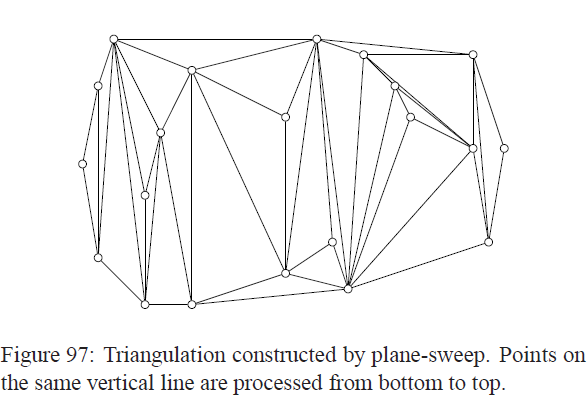
大家自己画一个草图就可以验证一下了。我们可以在O(n^2)的时间内两两检验,但是否可以更快呢?事实上用平面扫描的方法就可以。为了方便,我们假设没有一条线段为铅垂线且没有重合的端点。我们维护一个集合,集合内都是和我们的扫描线相交的线,他们顺序按照遇到扫描线的顺序排列。只有那些相邻的线段才会被用来检验是否相交。因为两条相交的线始终是在都遇到扫描线之后才相交。完整的算法参考下面代码:


Delaunay Triangulations:
用平面扫描得到的三角剖分实际上性质不太好,因为有很多细长的三角形出现,所以会有不少很大的角和很小的角。然而我们要介绍的这个新的三角剖分有着更好的性质,一方面保证速度快,另一方面尽可能地减少那些不太好的角。
首先来看一下平面扫描得到的三角剖分和我们的新算法产生的三角剖分之间的差别,下面是一个例子。

接下来我们介绍一下维诺图,这个图的核心在于借助所有点的集合S进行平面的划分,对于每一个S中的元素u,我们划分Vu = {x∈R^2 | ||x - u|| <= ||x - v||, 任意v∈S},也就是说Vu中的点到u的距离不大于到其他任何点的距离。下面是一个例子,其中每一个实线圈出的一个图形称作维诺区域,而整个维诺图是维诺区域合并所得:
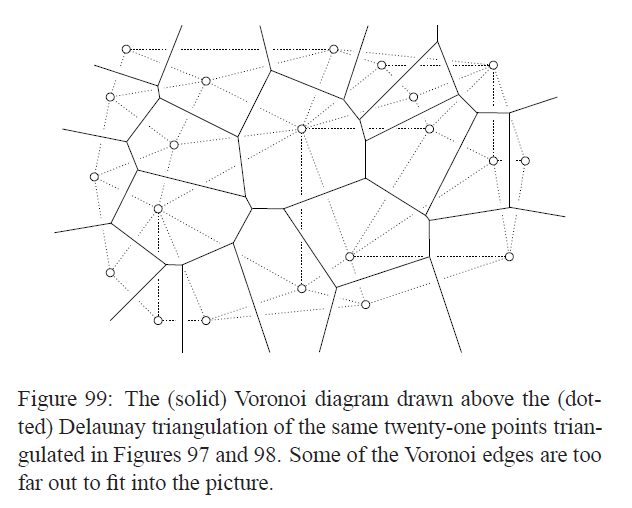
值得注意的是维诺图的部分是无法画出来的,因为涉及无穷远处。有三条重要的性质:1、维诺区域是有边界的当且仅当我们选择的点u位于凸包S的内部;2、维诺图有两两不交的内部共同构成平面;3、每一个维诺区域都是由n-1(其中n为所有的顶点数量)个闭半平面交出来的。
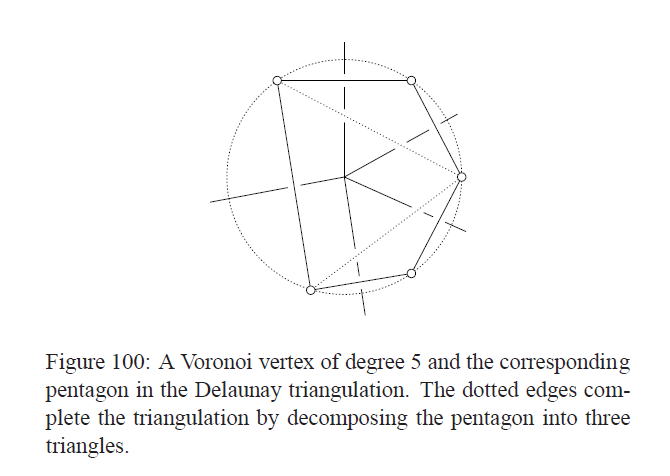
我们只要把相邻的维诺区域中的点连起来,就可以构成一个三角剖分。选中的维诺图中的顶点x至少有3个离他最近的S中的点,设为u,v,w;我们注意到x到这三个点的距离是一样的,换句话说可以构造一个本不存在的圆,其他所有的点都在这个圆的外面;或者每一条维诺图中的线都会在一个圆里面,而这条线的中点可以构造一个圆和其他线没有交点,这个性质可以来证明维诺图是一个平面图。下面是一个例子(这个图里面voronoi图中点的度数是5,大于3,所以要分割一下变成三角形):
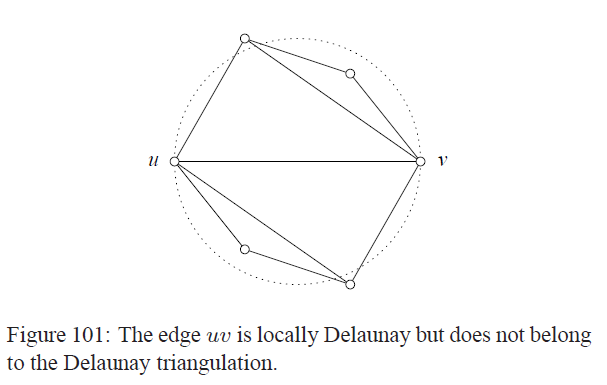
我们来提出局部Delanayhood的概念,说的是对于三角剖分里的一条边uv,如果它是三角区域的公共边设为u,v,p和u,v,q先然后u,v,p可以做一个外接圆,那么uv称为局部的Delanayhood的当且仅当q落在这个外接圆上或者在圆外。有一个Delanayhood的定理是说,三角剖分满足我们之前提出的构造方法(也成为Delanay 三角剖分)当且仅当所有的公共边都满足这个局部性质。下面是一个反例:
上面这个定理实际上启发我们,只要对任何一个三角剖分,都有变成我们想要的Delaunay剖分的可能,那就是对边进行变化(文中说是翻折),在下面这个例子里,我们发现uv不满足定理条件,于是我们进行flip操作,也就是把对角线对调,详情看下面的这个图:

于是我们只要遍历所有的边进行局部化处理就可以了。伪代码如下:

同时我们来研究一下怎么判断在第四个点是否在三个点形成的圆内。
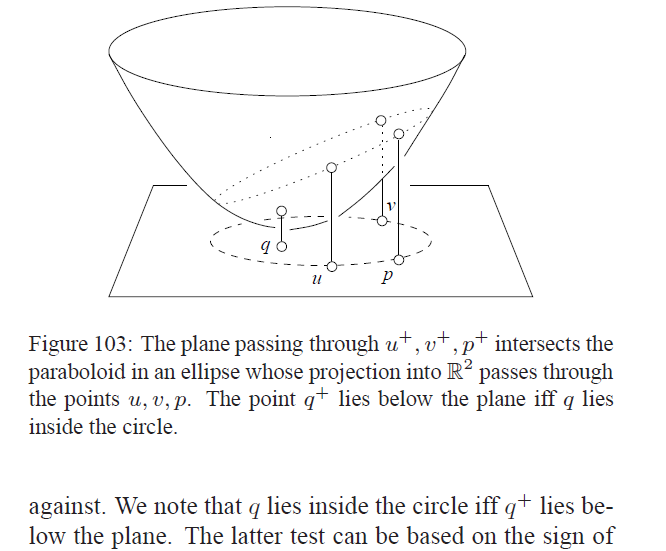
这里作一个图形是z = x^2 + y ^2,那么q位于u,v,p的外接圆内当且仅当q+在上面的截面之下。其中截面是把z = x^2 + y^2移上去的之后得到。我们可以通过相乘下面两式判断符号来做推断:



Alpha Shapes:
很多的几何应用都和一个有限的点集合的直观而又模糊的形状概念有关系。为了使得这个概念更加清晰,我们用点对之间的距离来确定Delaunay三角剖分的子复杂度(不同的解决方案有不同的形状)。
首先来介绍圆盘的并,令S为点集合,Bu(r) = {x | ||x - u|| <= r},是一个以u为圆心,r为半径的闭圆盘。Ru(r) = Bu(r)∩Vu,得到了u对应的区域:一个维诺区域和圆盘的交集。U(r) = 所有Bu(r)的并。我们说Ru(r)满足下面的性质:1)Ru(r)对于每个S中的u和r都是一个闭的凸区域,2)不同点对应的Ru(r)是不一样的,3)U(r) = 所有Ru(r)的并集。要注意的是这里面的r是可以变的。
我们之前先介绍了维诺图,然后介绍了Delaunay三角划分;类似的,我们对圆盘的维诺分解,介绍一个alpha复合体。我们先定义一个"nerve"的概念,设集合C的元素是一系列集合,那么NrvC = {X包含于C | ∩X ≠ 空}。这是一种抽象的简单复合体,因为如果X满足上面的条件的话,那么X的子集也会满足这个条件,因为∩X包含于∩Y。我们说NrvC是Delaunay三角划分的一个抽象实现版本,而后者为前者的几何实现,严格的来讲,当一个圆上没有四个点的时候,这个是正确的。Alpha(r) = Nrv{Ru(r) | u ∈ S},详情见下图:
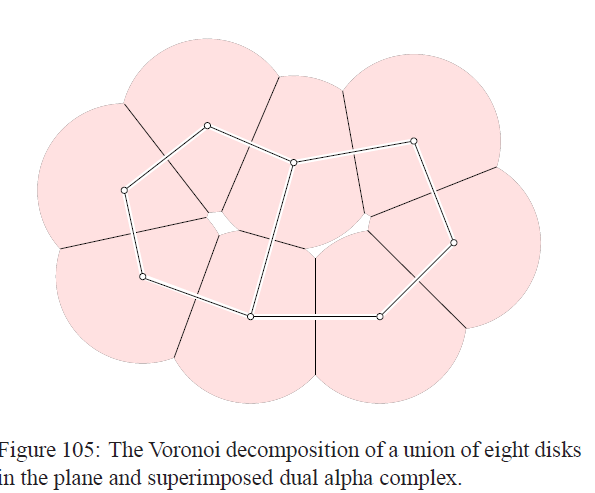
上图中,我们称这种关于半径r的Alpha(r)的几何实现为A(r),其中alpha shape是A所占据的空间。我们对那些alpha shape对应的几何形状感兴趣,实际上随着r变大,我们的A(r)会变大,这样一来我们会得到下面的图形:
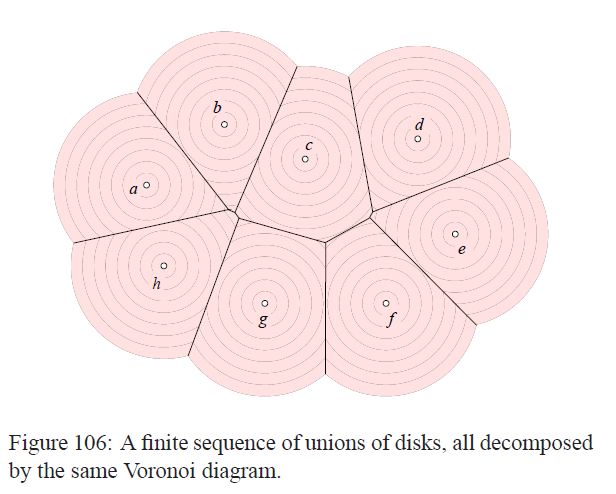
这样一来我们就会得到一系列的Alpha complexs。我们可以一步步地加入线条使得其被分割。
Homework:



