Geometric Graphs:
我们把一个图的边还原到了直觉中的曲线,来构造一个新的图。
首先提出了embedding的概念,由映射f: V -> R^2决定,要求V中不同的顶点映射到不同的点,曲线不自交,曲线形成的点只有V映射过来的点,两条曲线最多在端点处相交(意味着最多一个交点)。我们始终可以把一个图映射到三维空间且保持嵌入的性质,换句话说,二维空间不一定有这个性质。我们称一个图是平面图如果它有2维嵌入,之后可以看到一个图有2维嵌入时就会有一个直线嵌入(每条边都是线段)。
欧拉公式:n = |V|, m = |E|, l为面的个数,我们有n - m + l = 2;极大平面图是指那些加入任何一条边后都会破坏平面性质的平面图。根据欧拉公式和极大平面图的握手定理可以得到m = 3n - 6,l = 2n - 4(n>=3)。库拉图斯基定理是说一个图G是一个平面当且仅当这个图m没有和K5和K3,3同构的子图。
我们由最大平面图的边数可以得到一个最大平面图总会有一个顶点的度数小于等于5(n>=3),接下来我们介绍Fary's构造,也就是每一个平面图都有一个直线嵌入。方法如下:如果只有三个顶点就已经搞定了;否则选择一个度数为k且 k小于等于5的顶点,把他删去剩下n - 1个顶点,m = 3n - 6 - k,此时3(n-1) - 6 - (3n-6-k) = k-3,再加入k-3条边使得其变成极大平面图,然后递归地进行操作,然后去掉加入的k-3条边还原删掉的顶点和对应的边。下面这个图是一个漂亮的例子:
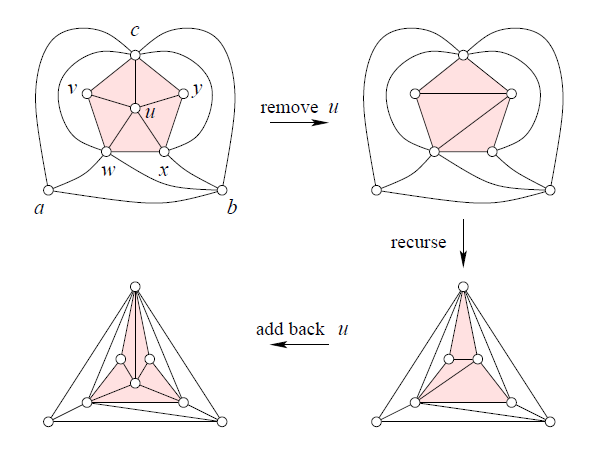
Tutte's construction:这是一个更加有效的构造直线嵌入的方法,由Tutte提出。我们先来提出一个定义,一些顶点x1~xj(二维平面),那么这些顶点的平均值记为x。构造方法如下,我们先找到一个图G的三角形,顶点为a,b,c,对于除去这三个点的所有顶点分别执行一下操作:对每个点把它变成其他所有相邻点的平均值。这样就得到了一个直线嵌入,证明有点复杂。
Surfaces:
图形可以在1维,2维,3维甚至更高维的空间里绘制,但是它们的本质都是1维的,向上一步,我们可以发现所谓的表面,实际上都是2维的。先来介绍一下拓扑的2-流形概念,最简单的表面是那些看上去和实平面类似的例子,一个空间M是2维流形,如果其中的任何一点都存在一个邻域使得其局部同胚到R^2,特殊的,如果存在一个连续双射:N(x) -> R^2 且其逆映射也是连续的,那么就是一个同胚。像2维的开圆盘,球面等都是2维流形;但是前一个例子即开圆盘并不是一个紧集,因为它存在开覆盖没有有限覆盖,此时我们如果加上圆盘的边界,就可以去证明边界上的点存在领域同胚与H = {(x1,x2)|x1 >= 0},也就是半个平面,我们称这样的空间是带边界的2维流形。边界是那些邻域同胚于H的点的集合的子集,这是一个1维流形(每一个点都局部同胚于R)。特殊的是那些紧的首尾连接的1维流形,他们都是同胚于单位圆的(注意同构的流形之间我们不加区别)。一个紧的二维流形的标准表示方法是用彼此连接的三角形,一个“边、角、三角形”的集合称为紧2维流形的三角定位,如果满足下面两个条件:
1、集合里的每一个三角形,它的三条边都在集合内;每一条边的两个顶点都在集合内
2、每一条边都恰好属于两个三角形,每一个顶点都属于一系列的三角形
为了简化语言,我们可以用单纯形来表示集合中的元素,单纯形的维数有0,1,2。我们规定顶点是0维的,边是1维的,三角形是2维的。同时定义face的概念,一个单纯形的face是那些包含于它的单纯形的集合,所以条件1可以变成集合中每个单纯形的face都在集合中。同时我们定义star的概念,一个单纯形的star是那些face中包含此单纯形的单纯形,所以条件2可以转换为:每一个单纯形的star都同胚于R^2。为了存这样的结构,我们来看下面这个图:
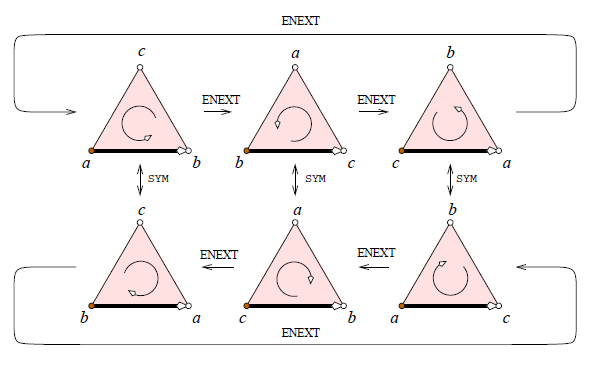
这是一个三角形的对称群的同构形式,也就是abc, bca, cab,bac, cba, acb(每个三角形有一个lead vertex和一条lead edge),我们对这个6点结构赋值为0,1,2,4,5,6。就可以从一个结构变化到另外一个结构。下面是一些例子:
ordTri ENEXT(u,l): if l <= 2 then return (u, (l+1) mod 3) else return (u,(l+1) mod 3 + 4) end if ordTri SYM(u,l): return (u,(l+4) mod 8) #得到lead vertex用ORG(u,l),得到有公共lead edge边的三角形用FNEXT(u,l)
接着介绍了一个2维流形是否是定向的(也就是数学分析中双侧曲面)的概念。比如之前的莫比乌斯带就是单侧曲面。
我们说两个相邻的三角形是方向一致的如果他们的shared edge的方向不同。用dfs的方法来解决这个问题:

(还有一部分内容太抽象了,之后有时间再看)
Homology:
在拓扑中,主要关注点并不是几何图形的size,而是一个空间是否是连通的。一些最基本的概念区分我们是否可以从一个地方到另一个地方。比如沿着某个障碍物走是否有一个环,在空间中是否有空洞等等,homology是这类的问题的正式表示。
首先是圈秩的概念,一个连通图G顶点数是n,边数是m的话,那么圈秩是m - (n-1)。因为一棵生成树的边数是n - 1,然后任意加一条边都会产生一个圈,而且两两圈都不一样。
之后是关于的群的数学内容,吃不消了。
Homework:
挑1题吧。
