今天看了一下高级数据结构（主要是多维数组、广义表、AVL树、Splay树）的内容，AVL树的部分之前提过了就不讲了，参见《红黑树和AVL树》，挑了一些觉得重要或有意思的点写在这里，希望有错误的地方请不吝指正。
1、三元组存取稀疏矩阵（较多元素为0），以及使用十字链表的方式来记录稀疏矩阵
2、注意广义表中的head、tail两个概念，以及深度、长度的概念；
对于L = (x0,x1,…,xn), head(L) = x0，tail(L) = (x1,x2,…,xn)
3、区分广义表中的纯表、再入表、循环表（深度为∞）等概念
纯表：任何元素（原子/子表）只能出现1次（类似正常的树结构）
再入表：表中元素可以重复出现（类似树结构中兄弟结点可以连线）
循环表：表中有回路，深度为无穷大
4、线性表 <= 纯表（树）<= 再入表（兄弟结点之间有连线） <= 图
5、最佳BST树的平均访问长度，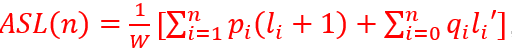
，其中pi表示内部节点的索引频率，qi表示外部结点的索引频率，pi/w或者qi/w表示对应的索引概率，要注意的是li + 1和li’之间的区别！其中li和li’都是路径长度，在等概率条件下可以得到 ASL(n) = (2I +3n)/(2n+1)，其中I是内部路径长度总和，所以要求ASL最小的话尽可能地I要小，此时也就是整棵树要接近完全二叉树。注意此处的一个大前提是等概率索引。
6、在不是等概率访问的前提下构建最佳BST树的算法依据是最佳BST树的子树仍然是最佳BST树，所以有最优子结构，因此可以采用动态规划的算法进行求解。只要在小区间里枚举相应的根节点并取出最小的就可以了。具体的例子：四个关键码为B、D、H、F，访问频率为1，5，4，3；且5个外部结点的访问频率为5，4，3，2，1。
随便写了一个代码仅供参考：
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #define N 100000000 5 using namespace std; 6 int n, p[105], q[105], dp[105][105];//p为内部结点,q为外部结点,dp[i][j]表示从i~j的代价最小的BST树 7 int sum(int i, int j){ 8 int m = 0; 9 for(int k = i; k <= j; k++)m += (p[k] + q[k]); 10 return (m + q[i - 1]); 11 } 12 int main(){ 13 cin >> n; 14 for(int i = 1; i <= n ;i++){ 15 cin >> p[i]; 16 } 17 for(int i = 0; i <= n; i++){ 18 cin >> q[i]; 19 } 20 for(int i = 0; i <= n ;i++){ 21 for(int j = 0; j <= n; j++){ 22 dp[i][j] = N; 23 } 24 } 25 //读入n个内部节点和n+1个外部结点的访问频率 26 for(int i = 1; i <= n; i++)dp[i][i] = p[i] + q[i - 1] + q[i];//单节点代价 27 for(int len = 2; len <= n ; len++){ 28 for(int s = 1; s + len - 1 <= n; s++){ 29 int e = s + len - 1;//dp[s][e] 30 printf("s = %d ,e = %d ", s, e); 31 for(int root = s; root <= e; root++){//枚举根节点 32 if(root > s && root < e) 33 dp[s][e] = min(dp[s][e], dp[s][root - 1] + dp[root + 1][e] + sum(s,root - 1) +p[root]+ 34 sum(root + 1, e)); 35 else if(root == s){ 36 dp[s][e] = min(dp[s][e], dp[root + 1][e] + p[root] + q[root - 1] + sum(root + 1,e)); 37 } 38 else{ 39 dp[s][e] = min(dp[s][e], dp[s][root - 1] + p[root] + q[root] + sum(s,root - 1)); 40 } 41 } 42 } 43 } 44 return 0; 45 }
（原来还有插入代码这种高级的操作，感谢平台）
7、Trie结构：改变关键码划分的方式，key通常是字符串，是一种有序树。基本性质有：1）根节点不包含字符，2）除根节点外每一个结点只包含一个字符，3）从根节点到某一结点的路径上字符连接起来得到该节点的字符串，4）每个节点的子节点包含的字符串都不一样，见下面的图示：
8、在Trie树中查找结点的效率和树中包含的结点数量没有关系，只和待查找的那个字符串的长度有关，这和AVL树不一样，比如一个长度5的字符串“ababa”，在AVL中需要log2(26**5) = 23.5次比较，在trie只要5次比较，但是trie树是不平衡的，比如t下单词比z下的单词多的多，且不利于检索（26个分支）。应用场所：前缀匹配、词频统计、排序。
9、由于数据访问的规则，大多数的数据并不会被访问，所以有了伸展树（一种自组织的数据结构），数据随检索而调整位置。是对BST的改进，但是不能保持AVL中的平衡条件。
10、访问一次结点x就把x展开，插入时把x移动到根节点，删除时把x的父节点移动到根节点。还是分为单旋转和双旋转（直接提升），一般来说，一字型旋转不会改变树的高度，但是之字形旋转会把树的高度减1，更加平衡。
11、伸展树不能保证每次访问都是有效率的，也就是访问可能是O(N)的，但是能够保证m次操作总共需要O(mlogN)的，也就是平均代价是O(logN)；严格的证明要用到摊还分析的方法，设x为一棵子树的根，S(x)为这棵树的总共节点数，u(x) = log2(S(x))，当前Splay树的势能定义为所有结点的u(x)之和，分别考虑zig/zag, zigzig/zagzag, zigzag/zagzig这六种操作，实际上考虑三个情况就行，不难发现每次旋转都是以c * (u(x’) – u(x)) + 1为上界，而且只有单纯的zig/zag才会用到1这个值，其余情况下c = 3就足够了，于是一次splay可以证明是O(log2n)的，m次Splay的总摊还代价是O(m*log2n + nlog2n)（后面是由势能提供的）。
关于splay树的复杂度分析，参考文章：https://max.book118.com/html/2017/0623/117570994.shtm