方差分析--实践

一、案例：

有A、B、C、D四个地区，不同地区的销售量不一样，现抽取了不同时间段内每个地区的销售量，试解决：

1、每个地区间的销售量是否相同？

2、不同月份的销售量是否相同？

3、不同时间与地区的销售量是否相同？

二、数据：

 问题1：

用单因素方差分析，先假设，再构造统计量，最后进行决策
（1）假设H0，即假设样本A,B,C,D的均值相同，不同地区无显著性影响。H1：样本A,B,C,D均值不全相等，有显著性影响。
​（2）构造统计量，因素为地区，水平为4，因变量为销售量。

import numpy as np
import scipy.stats as stats
import pandas as pd
#读取数据
data=pd.read_excel("销售数据.xlsx")

print(data.describe())  #统计数量、均值、标准差、上下四分位
print(data.mean().sum()/4)  #输出对应的总体均值

总平方和SST＝95533231.1875+61867762.1875+86597368.1875+36583242.6875
组间平方和SSA=57894573.5196352
组内平方和SSE=222687030.727273
MSA=SSA/(4-1)=19298191.17 , MSE =SSE/(N-K)=31812432.96,
检验统计量F=MSA/MSE=0.606624184 , 在给定显著性水平a=0.05,在F分布表中查找分子自由度df1=4-1=3,分母自由度df2=n-k=11-4=7,相应的临界值Fa(3,7)=4.347,F<Fa 则不拒绝原假设H0,即认为各地区对销售量影响不显著。

问题2：

1）假设H0:各月的均值相等，即各个月份对销售量无显著影响；H1:各个月份均值不完全相同，即不同月份对销售量有显著影响。

（2）构造和计算统计量
(所有数据按照月份分组,2019年3月数据少4行，因此保留前12行分析数据）
1)计算总体均值：5898.5，水平为3
2)总平方和SST=205887565
3)组间平方和SSA=39687746
4)组内平方和SSE=SST−SSA=205887565−39687746=166199819
5）MSA=SSA/(3-1)=19843873
MSE=SSE/(n-k)=SSE/(12-3)=18466646.56
6)F=MSAMSE=1.074579131
(3)决策分析，F<Fa=Fa(2,9)=4.256，不拒绝原假设，即各个月份影响不显著。

问题3：

按照无交互作用的双因素方差分析方法
（1）假设（2）构造统计量和计算（3）决策

（1）行因素：H0:假设日期对销售量无显著影响；H1:日期对销售量有显著影响;
列因素：H0:假设地区对销售量无显著影响H1:地区对销售量有显著影响列因素。
（2）构造统计量并计算：

 

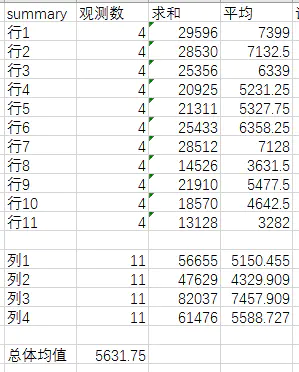
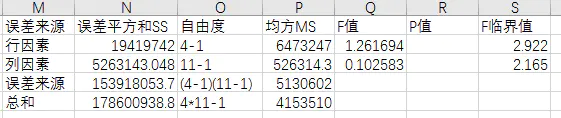
 (3)从上表中可以看出Fr<Fa，Fc<Fa，分别从地区、日期都对销售量影响不显著。

转自：https://www.jianshu.com/p/e248bdd18edc