一、关于体温、性别、心率的临床数据
对男性体温抽样计算下95%置信区间总体均值范围。转自:https://www.jianshu.com/p/a3efca8371eb
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt #读取数据 df = pd.read_csv('http://jse.amstat.org/datasets/normtemp.dat.txt', header = None,sep = 's+' ,names=['体温','性别','心率']) #选取样本大小,查看数据 np.random.seed(42) #df.describe() #样本量为90,查看样本数据 df_sam = df.sample(90) df_sam.head() #计算抽取样本中男士体温的均值 df3 = df_sam.loc[df_sam['性别']==1] df3['体温'].mean() #重复抽取样本,计算其他样本中男士体温的均值,得到抽样分布 boot_means = [] for _ in range(10000): bootsample = df.sample(90, replace=True) mean = bootsample[bootsample['性别'] == 1]['体温'].mean() boot_means.append(mean) #绘制男士体温抽样分布均值 #计算抽样分布的置信区间以估计总体均值, 置信度95% np.percentile(boot_means, 2.5), np.percentile(boot_means, 97.5)
二、python实现一个总体均值的置信区间
转自:https://blog.csdn.net/qq_39284106/article/details/103707239

def mean_interval(mean=None, std=None, sig=None, n=None, confidence=0.95): """ mean:样本均值 std:样本标准差 sig: 总体方差 n: 样本量 confidence:置信水平 功能:构建总体均值的置信区间 """ alpha = 1 - confidence z_score = scipy.stats.norm.isf(alpha / 2) # z分布临界值 t_score = scipy.stats.t.isf(alpha / 2, df = (n-1) ) # t分布临界值 if n >= 30 and sig != None: me = z_score*sig / np.sqrt(n) # 误差 lower_limit = mean - me upper_limit = mean + me if n >= 30 and sig == None: me = z_score*std / np.sqrt(n) lower_limit = mean - me upper_limit = mean + me if n < 30 and sig == None: me = t_score*std / np.sqrt(n) lower_limit = mean - me upper_limit = mean + me return (round(lower_limit, 3), round(upper_limit, 3)) mean_interval(mean=8900, std=None, sig=500, n=35, confidence=0.95) mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.90) mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.99)
三、实现一个总体方差的置信区间
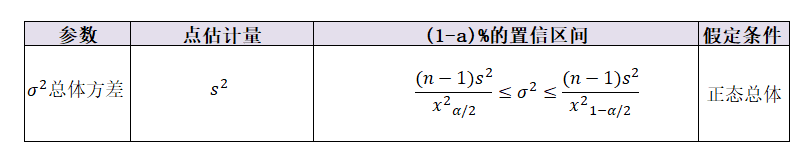
(1) 样本均值为21, 样本标准差为2, 样本量为50; (2) 样本均值为1.3, 样本标准差为0.02, 样本量为15; (3) 样本均值为167, 样本标准差为31, 样本量为22; Question1: 根据以上样本结果,计算总体方差的90%的置信区间? Question2: 根据以上样本结果,计算总体标准差的90%的置信区间? def std_interval(mean=None, std=None, n=None, confidence=0.95, para="总体标准差"): """ mean:样本均值 std:样本标准差 n: 样本量 confidence:置信水平 para:总体估计参数 功能:构建总体方差&总体标准差的置信区间 """ variance = np.power(std,2) alpha = 1 - confidence chi_score0 = scipy.stats.chi2.isf(alpha / 2, df = (n-1)) chi_score1 = scipy.stats.chi2.isf(1 - alpha / 2, df = (n-1)) if para == "总体标准差": lower_limit = np.sqrt((n-1)*variance / chi_score0) upper_limit = np.sqrt((n-1)*variance / chi_score1) if para == "总体方差": lower_limit = (n-1)*variance / chi_score0 upper_limit = (n-1)*variance / chi_score1 return (round(lower_limit, 2), round(upper_limit, 2)) std_interval(mean=21, std=2, n=50, confidence=0.90) std_interval(mean=1.3, std=0.02, n=15, confidence=0.90) std_interval(mean=167, std=31, n=22, confidence=0.90)
四、实现两个总体方差比的置信区间
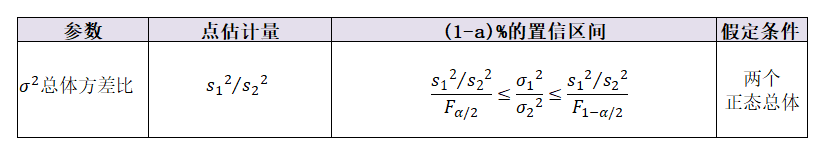
data1 = [3.45, 3.22, 3.90, 3.20, 2.98, 3.70, 3.22, 3.75, 3.28, 3.50, 3.38, 3.35, 2.95, 3.45, 3.20, 3.16, 3.48, 3.12, 3.20, 3.18, 3.25] data2 = [3.22, 3.28, 3.35, 3.38, 3.19, 3.30, 3.30, 3.20, 3.05, 3.30, 3.29, 3.33, 3.34, 3.35, 3.27, 3.28, 3.16, 3.28, 3.30, 3.34, 3.25] def two_std_interval(d1, d2, confidence=0.95, para="两个总体方差比"): """ d1: 数据1 d2: 数据2 confidence:置信水平 para:总体估计参数 功能:构建两个总体方差比&总体标准差比的置信区间 """ n1 = len(d1) n2 = len(d2) var1 = np.var(d1, ddof=1) # ddof=1 样本方差 var2 = np.var(d2, ddof=1) # ddof=1 样本方差 alpha = 1 - confidence f_score0 = scipy.stats.f.isf(alpha / 2, dfn=n1-1, dfd=n2-1) # F分布临界值 f_score1 = scipy.stats.f.isf(1-alpha / 2, dfn=n1-1, dfd=n2-1) # F分布临界值 if para == "两个总体标准差比": lower_limit = np.sqrt((var1 / var2) / f_score0) upper_limit = np.sqrt((var1 / var2) / f_score01) if para == "两个总体方差比": lower_limit = (var1 / var2) / f_score0 upper_limit = (var1 / var2) / f_score1 return (round(lower_limit, 2), round(upper_limit, 2)) two_std_interval(data1, data2, confidence=0.95, para="两个总体方差比")