python数据分析之数据分布

转自链接：https://blog.csdn.net/YEPAO01/article/details/99197487

一、查看数据分布趋势

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#读取源数据
df = pd.read_csv('http://jse.amstat.org/datasets/normtemp.dat.txt', header=None, sep='s+', names = ['体温','性别','心率'])
df.head()

  #下载到本地
　　re = requests.get("http://jse.amstat.org/datasets/normtemp.dat.txt")
　　re.encoding = "utf-8"
　　with open("normtemp.dat.txt","w") as f:
　　f.write(re.text)
　　df = pd.read_csv("normtemp.dat.txt", header=None, sep="s+")
　　df.columns = ['体温','性别','心率']
　　df.head()
  #2 不下载
　　columns = ['体温','性别','心率']
　　df = pd.read_csv("http://jse.amstat.org/datasets/normtemp.dat.txt", header=None, sep="s+")
　　df.columns = ['体温','性别','心率']

#查看数据基本特征
df.describe()

绘制散点图

# 散点图
fig = plt.figure(figsize=(16,5))
df1 = df[df["性别"]==1]
df1.shape
plt.scatter(df1.index, df1["体温"], c="r", label="male")
plt.legend()
df2 = df[df["性别"]==2]
df2.shape
plt.scatter(df2.index, df2["体温"], c="b", label="female")
plt.legend()
plt.ylabel("tw")
plt.xlabel("x")
plt.grid()

 柱形图

# 柱形图
x = np.arange(0,130,1)
y = df_tw.values
plt.bar(x,y)

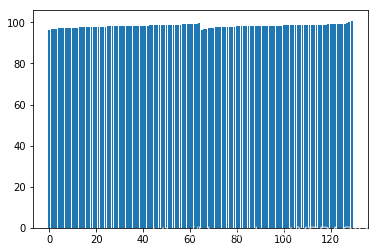
绘制直方图查看体温分布趋势

 df_tw.hist(bins=20,alpha = 0.5) df_tw.plot(kind = 'kde', secondary_y=True) 

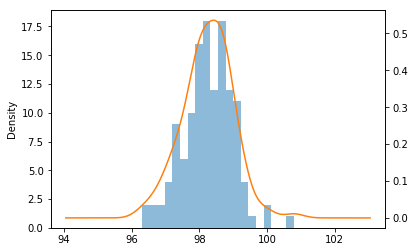
计算温度个数

# 针对温度数据, 计算温度的个数
df_tm01 = df_tm.value_counts() # 计数
df_tm01.sort_index(inplace=True) # 按照温度排序
print(df_tm01.head())


96.3    1
96.4    1
96.7    2
96.8    1
96.9    1
Name: 体温, dtype: int64

plt.scatter(df_tm01.index,df_tm01.values)

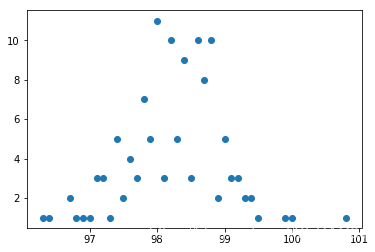
 检验是否符合正太

方法1 ：scipy.stats.normaltest (a, axis=0)
参数：a - 待检验数据；axis - 可设置为整数或置空，如果设置为 none，则待检验数据被当作单独的数据集来进行检验。该值默认为 0，即从 0 轴开始逐行进行检验。
返回：k2 - s^2 + k^2，s 为 skewtest 返回的 z-score，k 为 kurtosistest 返回的 z-score，即标准化值；p-value - p值

import scipy.stats
scipy.stats.normaltest(df_tm)


NormaltestResult(statistic=2.703801433319236, pvalue=0.2587479863488212)

得到的p值>0.05

方法2 Shapiro-Wilk test
方法：scipy.stats.shapiro(x)
官方文档：SciPy v1.1.0 Reference Guide
参数：x - 待检验数据
返回：W - 统计数；p-value - p值

scipy.stats.shapiro(df_tm.values)

(0.9865770936012268, 0.233174666762352)

得到的p值 0.23 > 0.05, 符合正态分布

方法3: scipy.stats.kstest

方法：scipy.stats.kstest (rvs, cdf, args = ( ), N = 20, alternative =‘two-sided’, mode =‘approx’)
官方文档：SciPy v0.14.0 Reference Guide
参数：rvs - 待检验数据，可以是字符串、数组；
cdf - 需要设置的检验，这里设置为 norm，也就是正态性检验；
alternative - 设置单双尾检验，默认为 two-sided
返回：W - 统计数；p-value - p值

u = df_tm.mean()
std = df_tm.std()
scipy.stats.kstest(df_tm.values,'norm',args=(u,std))

KstestResult(statistic=0.06472685044046644, pvalue=0.6450307317439967)

方法4: Anderson-Darling test
方法：scipy.stats.anderson (x, dist =‘norm’ )
该方法是由 scipy.stats.kstest 改进而来的，可以做正态分布、指数分布、Logistic 分布、Gumbel 分布等多种分布检验。默认参数为 norm，即正态性检验。
官方文档：SciPy v1.1.0 Reference Guide
参数：x - 待检验数据；dist - 设置需要检验的分布类型
返回：statistic - 统计数；critical_values - 评判值；significance_level - 显著性水平

scipy.stats.anderson(df_tm.values,dist="norm")


AndersonResult(statistic=0.5201038826714353, critical_values=array([0.56 , 0.637, 0.765, 0.892, 1.061]), significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]))

结论:三种检验的pvalue值均大于5%，因此体温值服从正态分布。第四种方法返回的不是pvalue值.

使用箱型图查看是否存在异常值.

#箱型图
df_tm.plot.box(vert=False, grid = True)

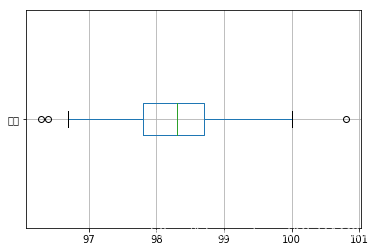
 查找具体的异常值数据

# 上四分位数
q3 = df_tm.quantile(q=0.75)
#下四分位数
q1 = df_tm.quantile(q=0.25)
# 四分位差
iqr = q3-q1
print("上四分位数:{}
下四分位数:{}
四分位差{}".format(q3,q1,iqr))
df_tm_01 = df_tm[(df_tm>q3+1.5*iqr) | (df_tm<q1-1.5*iqr)]
print("异常值:
{}".format(df_tm_01))

上四分位数:98.7
下四分位数:97.8
四分位差0.9000000000000057
异常值:
0       96.3
65      96.4
129    100.8
Name: 体温, dtype: float64

利用python计算两者之间的相关性系数
需要了解统计学三大相关系数: 绝对值越大，相关性越强

pearson
kendall
spearman
相关系数 相关强度
0.8-1.0 极强
0.6-0.8 强
0.4-0.6 中等
0.2-0.4 弱
0.0-0.2 极弱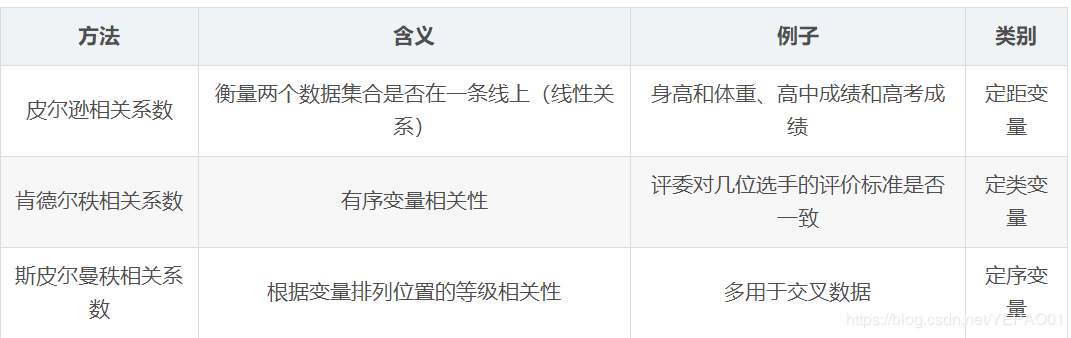

#相关系数
df["体温"].corr(df["心率"], method='pearson')
0.24328483580230698

# spearman 相关系数
df["体温"].corr(df["心率"], method='spearman')
0.265460363879611

# kendall 相关系数
df["体温"].corr(df["心率"], method='kendall')
0.17673221630037853

或

df = df[["体温","心率"]]
print(df.corr(method='pearson'),"
")
print(df.corr(method='spearman'),"
")
print(df.corr(method='kendall'),"
")

          体温        心率
体温  1.000000  0.243285
心率  0.243285  1.000000 

         体温       心率
体温  1.00000  0.26546
心率  0.26546  1.00000 

          体温        心率
体温  1.000000  0.176732
心率  0.176732  1.000000 

fig = plt.figure(figsize=(16,5))
plt.scatter(df.index, df["体温"])
plt.scatter(df.index, df["心率"])

参考链接https://blog.csdn.net/cyan_soul/article/details/81236124

---

二、python中实现数据分布的方法

参考链接：https://www.cnblogs.com/pinking/p/7898313.html

#二项分布
from scipy.stats import binom

#几何分布
from scipy.stats import geom

#泊松分布
from scipy.stats import poisson

#均匀分布
from scipy.stats import uniform

#指数分布
from scipy.stats import expon

#正太分布
from scipy.stats import norm