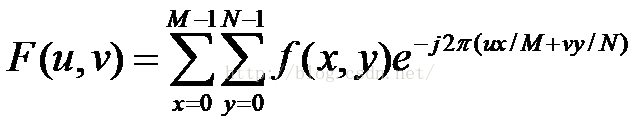在讲解对图像进行傅里叶变换之前,我们先来了解一下傅里叶变换,毕竟也接近几年没有接触傅里叶变换了,也忘得差不多了。
一 傅里叶变换
傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)。
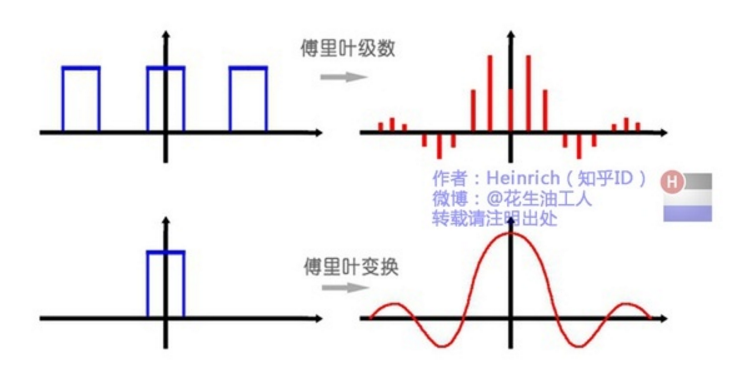
傅里叶级数:所有周期信号都可以分解为不同频率的各次谐波分量。
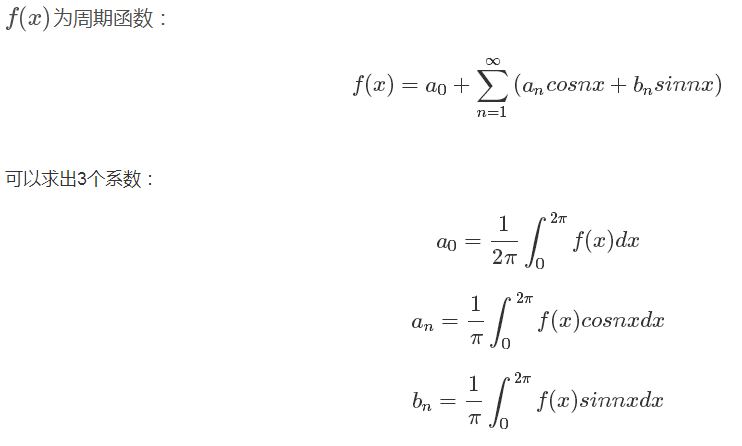
傅里叶变换:非周期信号可以看作不同频率的余弦分量叠加,其中频率分量可以是从0到无穷大任意频率,而不是像傅里叶级数一样由离散的谐波分量组成。

网上已经有很多关于傅里叶变换的经典文章了,这里推荐阅读:
傅里叶变换和傅里叶级数的区别与联系(后续更新补充DTFT、DFS)
二 图像的傅里叶变换
图像是一个二维的信号,所以对它进行二维的傅里叶变换,对于MXN的一幅图像的离散二维傅里叶变换,公式如下:
从公式上可以看出,F(u,v)与f(x,y)与并不是一一对应的关系,F(u,v)所对应的不是某一个f(x,y)而是所有的f(x,y)与e^(-j2*pi(ux/M+vy/N))的乘积的和。因此F(0,0)就是所有像素的平均和。(这里的求和我们可以看做是傅里叶变换中的积分)
参考文献
[1]图像的傅里叶变换