Codeforces 1090J $kmp+hash+$二分

题意

给出两个字符串(s)和(t)，设(S)为(s)的任意一个非空前缀，(T)为(t)的任意一个非空前缀，问(S+T)有多少种不同的可能。

Solution

看了一圈，感觉好像就我一个人写的(kmp+hash+)二分。

直接算好像不是很好算？先容斥一下，不同(=)总方案(-)相同。

显然总方案为两个字符串的长度的乘积，考虑相同的情况怎么算。

相同即两组(S)和(T)不同，但(S+T)本质相同的情况.

这个东西怎么算呢。。。。

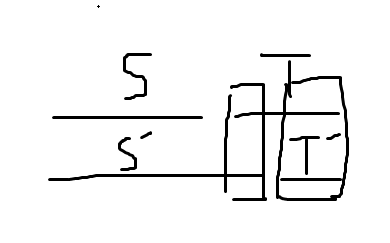
（感觉看图会好理解一点

不难想到当上图框出来的地方相同，则两者同质。

先来看右边那个框，显然这个东西就是一个字符串里两个子串([1,i],[j,k])相同。

左边这个框就是(s)的某个子串和(t)的前缀相同。

具体怎么算？

根据上图，设(a_i)为(t)的前缀([1,i])在(s)里出现了几次，这个可以(hash+)二分算。

设(b_i)为符合([1,j]=[i-j+1,i])的(j)的最大值，这个可以(kmp)一波。

那么最终同质的个数就是(sum_{i=2}^{|t|}a_{i-b_i})

#include<bits/stdc++.h>
#define For(i,x,y) for (register int i=(x);i<=(y);i++)
#define Dow(i,x,y) for (register int i=(x);i>=(y);i--)
#define cross(i,u) for (register int i=first[u];i;i=last[i])
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
    ll x=0;int ch=getchar(),f=1;
    while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar();
    if (ch=='-'){f=-1;ch=getchar();}
    while (isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
    return x*f;
}
const int N = 1e5+10;
int n,m;
char a[N],b[N];
const ull base = 233;
ull pre[N],Pre[N],p[N];
const ll Base = 23, mod = 1e9+7;
ll pre2[N],Pre2[N],p2[N];
inline void GetPre(){
	p[0]=1;For(i,1,n) p[i]=p[i-1]*base;
	For(i,1,n) pre[i]=pre[i-1]*base+a[i];
	For(i,1,m) Pre[i]=Pre[i-1]*base+b[i];
	p2[0]=1;For(i,1,n) p2[i]=p2[i-1]*Base%mod;
	For(i,1,n) (pre2[i]=pre2[i-1]*Base%mod+a[i])%=mod;
	For(i,1,m) (Pre2[i]=Pre2[i-1]*Base%mod+b[i])%=mod;
} 
inline ull query(int l,int r){return pre[r]-pre[l-1]*p[r-l+1];}
inline ll query2(int l,int r){return (pre2[r]-pre2[l-1]*p2[r-l+1]%mod+mod)%mod;}
int now,fail[N];
inline void GetKmp(){
	now=0;
	For(i,2,m){
		while (now&&b[now+1]!=b[i]) now=fail[now];
		fail[i]=(b[now+1]==b[i]?++now:now);
	}
}
int sum[N];
inline void Get(){
	For(i,2,n){
		int l=1,r=min(m,n-i+1),mid,ans=0;
		while (l<=r){
			mid=l+r>>1;
			if (query(i,i+mid-1)==Pre[mid]&&query2(i,i+mid-1)==Pre2[mid]) l=mid+1,ans=mid;
				else r=mid-1;
		}
		sum[ans]++;
	}
	sum[0]=0;
	Dow(i,m,1) sum[i]+=sum[i+1];
}
inline void calc(){
	ll ans=1ll*n*m;
	For(i,2,m) if (fail[i]) ans-=sum[i-fail[i]];
	printf("%lld
",ans);
}
int main(){
	scanf("%s",a+1),scanf("%s",b+1),n=strlen(a+1),m=strlen(b+1);
	GetPre(),GetKmp(),Get(),calc();
}