排序算法

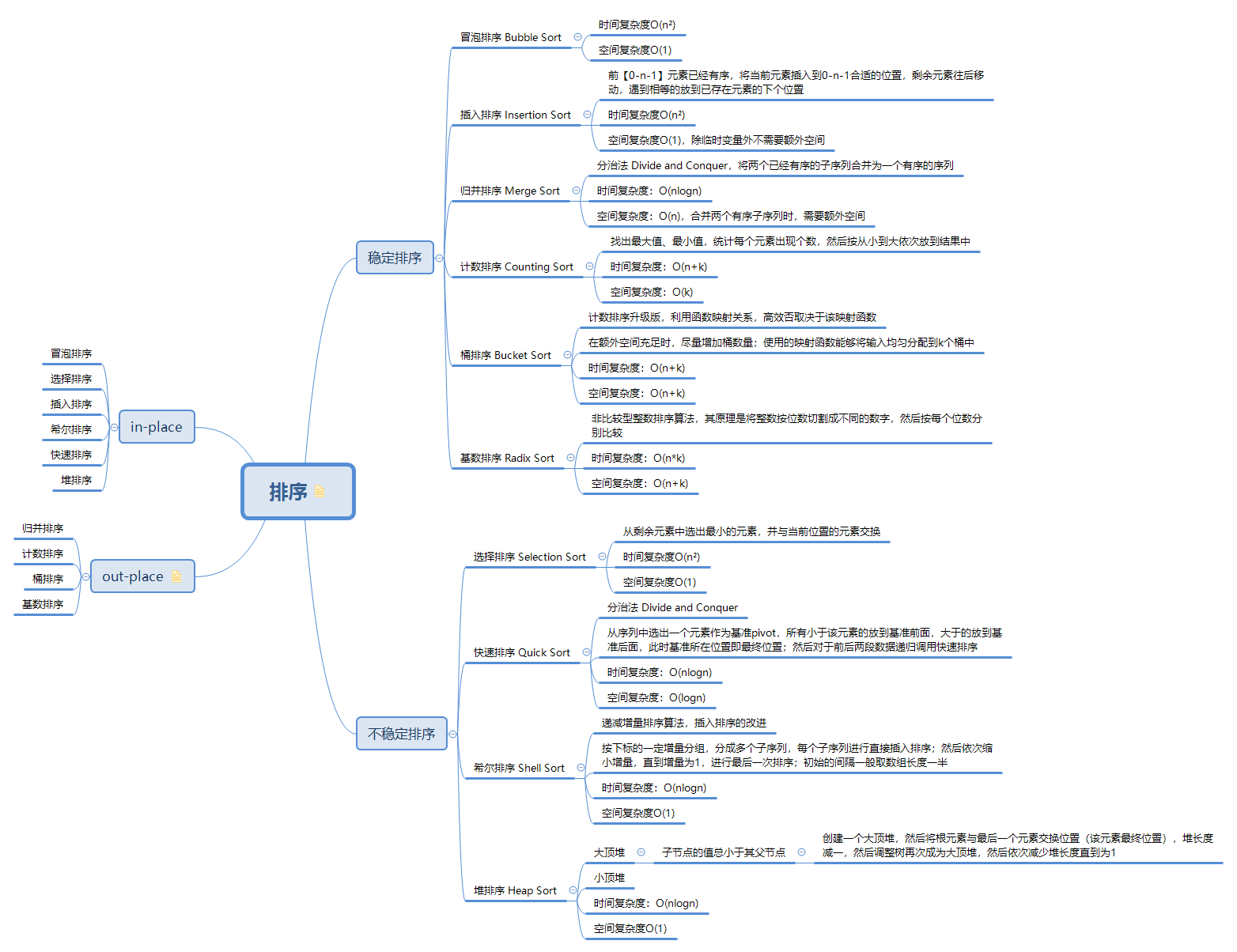
常见排序算法归纳如下：

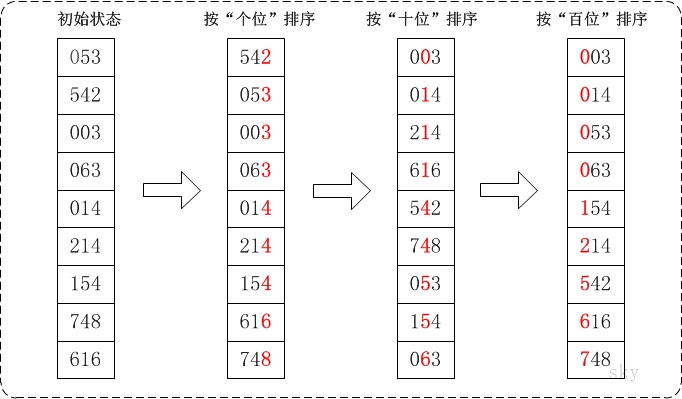
基数排序图文说明

通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}，它的示意图如下：

 冒泡排序：

最简单的排序算法， 两层for循环即可

插入排序：

　　对于元素 i 来说，0-i-1的元素已经完成了排序，需要在0- i-1 中找到合适的位置插入该元素即可。

void insertionSort2(int data[], int len)
{
    int tmp = 0;
    for (int i = 1; i < len; i++)
    {
        tmp = data[i];
        int j = i - 1;
        for (; data[j] > tmp; j--)
        {
            if (data[j] > tmp)            //稳定排序
                data[j + 1] = data[j];    //大于的元素依次向后移动一个位置;
        }
        data[j+1] = tmp;    //上面循环退出时，j元素值小于tmp，所以j+1=tmp
    }
}

希尔排序

升级版的插入排序算法，代码如下：

//插入排序的升级版，对于第i个元素，前面的元素（间隔interval）已经有序了
void shellSort(vector<int>& data)
{
    int length = data.size();
    int interval = length >> 1;

    while (interval >= 1)
    {
        //下面的两个for是插入排序逻辑
        for (int i = interval; i < length; i++)
        {
            for (int j = i; j >= interval; j -= interval)
            {
                if (data[j] < data[j-interval])
                {
                    //int tmp = data[j];
                    //data[j] = data[j - interval];
                    //data[j - interval] = tmp;//
                    swap(data[j], data[j - interval]);
                }
            }
        }
        interval = interval >> 1;        //每次修改interval
    }
}

归并排序Merge Sort

分治思想（Divide and Conque）

//分治思想，将序列分割为子序列（分割到最后为1个元素）
//子序列排序后再合并为一个有序的
void merge(vector<int>& data, int left, int mid, int right)
{
    //left - mid: 已经排序
    //mid+1 - right: 已经排序
    vector<int> leftVec(data.begin() + left, data.begin() + mid + 1);
    vector<int> rightVec(data.begin() + mid + 1, data.begin() + right + 1);
    
    int idx1 = 0;
    int idx2 = 0;
    for (int i = left; i <= right; i++)
    {
        if (idx1 == leftVec.size())
        {
            if (idx2 == rightVec.size())
                break;

            data[i] = rightVec[idx2++];
            continue;
        }
        if (idx2 == rightVec.size())
        {
            if (idx1 == leftVec.size())
                break;
            data[i] = leftVec[idx1++];
            continue;
        }

        if (leftVec[idx1] <= rightVec[idx2])
            data[i] = leftVec[idx1++];
        else
            data[i] = rightVec[idx2++];
    }
}

void mergeSort(vector<int>& data, int left, int right)
{
    if (left >= right)    //此时，递归时每个子序列只有1个元素了，然后调用merge
        return;
    int mid = (left + right) >> 1;
    mergeSort(data, left, mid);
    mergeSort(data, mid + 1, right);
    
    merge(data, left, mid, right);
}

选择排序

从剩余元素中选出最小的元素，并与当前位置的元素交换

//依次从剩余元素中选出最小的值，放到当前i位置
void selectionSort(vector<int>& data)
{
    int length = data.size();
    for (int i = 0; i < length; i++)
    {
        int min = INT_MAX;
        int idx = -1;
        for (int j = i; j < length; j++)
        {
            if (data[j] < min)
            {
                min = data[j];
                idx = j;
            }
        }
        
        if (i != idx)//交换 i j swap
        {
            int tmp = data[i];
            data[i] = data[idx];
            data[idx] = tmp;
        }
    }
}

快速排序

从序列中选出一个元素作为基准pivot，所有小于该元素的放到基准前面，大于的放到基准后面，此时基准所在位置即最终位置；然后对于前后两段数据递归调用快速排序