我们首先来看个线性同余方程:

如果对于方程 ax = b(a不为0),由于a存在倒数,因此很容易求解。如果在mod m的运算下,也有满足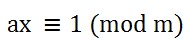 这样a的倒数一样的数存在的话,方程就有解了。而这个解x就叫做a关于m的逆元,记做
这样a的倒数一样的数存在的话,方程就有解了。而这个解x就叫做a关于m的逆元,记做 或是inv(a)。如果能求出逆元,那么就有x = inv(a) * ax = inv(a) * b, 就可以求出x了。
或是inv(a)。如果能求出逆元,那么就有x = inv(a) * ax = inv(a) * b, 就可以求出x了。
那么我们怎么求出inv(a)呢?
其实就是解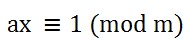
我们设ax = mt + 1;
移项得ax - mt = 1;
我们设y = -m,得ax + my = 1;
咦,这方程怎么那么眼熟,好像可用扩展欧几里得算法求得。
当然对于方程满足的条件必须是gcd(a, m) = 1,否则的话逆元是不存在的。
附上伪代码:
int gcd(int a, int b){
return !b ? gcd(b, a % b) : a;
}
int extgcd(int a, int b, int& x, int& y){
int d = a;
if(b != 0){
d = extgcd(b, a % b, y, x);
y -= (a / b) * x;
}
else x = 1, y = 0;
return d;
}
int inv(int a, int m){
int x, y;
int d = extgcd(a, m, x, y);
if(gcd(a, m) == 1)return (m + x % m) % m;
else return -1;//-1表示不存在逆元
}
当然,逆元还有其他的求法。在这之前我们需要知道一些姿势。
费马小定理:
在p是素数的情况下,对任意整数x都有
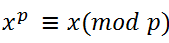
其中如果x不能被p整除则有:

继续变形:
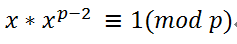
咦,我们发现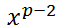 就是x关于p的逆元。即:
就是x关于p的逆元。即:
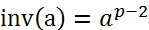
因此就可以用矩阵快速幂运算来求出逆元。
在不是素数的情况下, 我们也可以通过欧拉定理来求解。
欧拉定理:若a, n均为正整数,且a, n互质,则
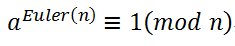
而费马小定理仅仅是其一个特例而已。
当然, 我们还可以用另外的方法。
我们知道p % b = p - (p / b) * b(这里的/表示整数除法ex : 7 / 2 = 3)
设x = p % b, y = p / b;
于是就有x + by = p;
我们两边同时取余p得(x + by) % p = 0;
x % p = (-y) * b % p;
x * inv(b) % p = (-y) % p;
inv(b) = (-y) * inv(x) % p;
inv(b) = (p - y) * inv(x) % p;
将x, y代入得:
inv(b) = (p - p / b) * inv(p % b) % p;
附上伪代码:
const int MOD = (int)1e9 + 7;//按题目要求的取余数
const int N = 1000000 + 5;
int inv[N + 5];
void init_inv(){
inv[1] = 1;
for(int i = 2; i < N; i ++)
inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
}