BZOJ 1064: [Noi2008]假面舞会（dfs + 图论好题！）

 http://www.lydsy.com/JudgeOnline/problem.php?id=1064

 题意：

思路：

考虑以下几种情况：

①无环并且是树：

无环的话就是树结构了，树结构的话想一下就知道它的k最大值就是它的最长链，最小值就是3（如果链长>=3的话），如果有多棵树，只需要把它们的最长链加起来即可。

②存在环并且顺序相同

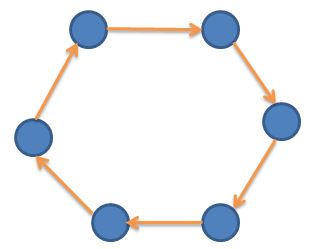
这种情况下的话k肯定是环长的约数，有多个环时就是它们之间的最大公约数。这样找最大和最小的约数即可。

③存在环并且顺序不同

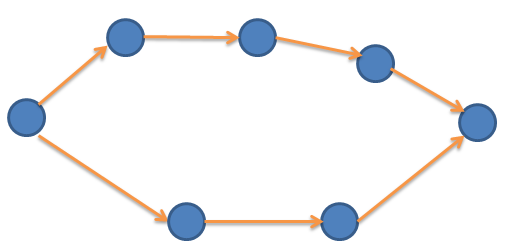
上面这个图的话就不是一个简单的单顺序的环了

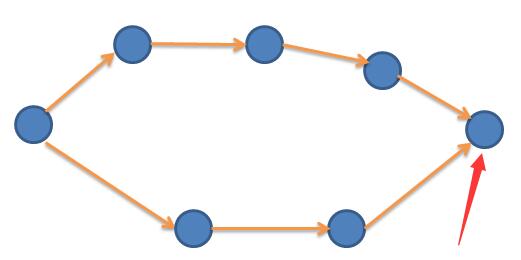
这个点只能有一个标号，但是它有两个点指向它，所以上面的链长和下面的链长模k必须相等。这也就是说在遍历的时候，如果碰到方向边，就应该链长-1。那么怎么实现呢？大神的做法是真的妙，对于每一条边，多加一条反向的边，赋值为-1。这样遍历时，就能计算出链长了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 100000+5;

int n,m,tot,ans,mx,mi;
int head[maxn],d[maxn];
bool vis[maxn], flag[maxn];

struct node
{
    int v,w,next;
}e[2000005];

void addEdge(int u, int v, int w)
{
    e[tot].v = v;
    e[tot].w = w;
    e[tot].next = head[u];
    head[u] = tot++;
}

int gcd(int a, int b)
{
    return b==0?a:gcd(b,a%b);
}

void dfs1(int u)
{
    vis[u] = 1;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v = e[i].v;
        if(!vis[v])
        {
            d[v] = d[u] + e[i].w;
            dfs1(v);
        }
        else ans = gcd(ans, abs(d[u] + e[i].w - d[v]));
    }
}


void dfs2(int u)
{
    mx = max(mx, d[u]);
    mi = min(mi, d[u]);
    vis[u] = 1;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v = e[i].v;
        if(!flag[i])
        {
            flag[i] = flag[i^1] = 1;
            d[v] = d[u] + e[i].w;
            dfs2(v);
        }
    }
}

int main()
{
    //freopen("in.txt","r",stdin);
    scanf("%d%d",&n,&m);
    tot = 0;
    memset(head,-1,sizeof(head));
    for(int i=0;i<m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        addEdge(u,v,1);
        addEdge(v,u,-1);
    }
    ans = 0;
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)
    {
        if(!vis[i])  dfs1(i);
    }
    if(ans)
    {
        int mi;
        if(ans<3)  puts("-1 -1");
        else
        {
            for(int i=3;i<=ans;i++)
            {
                if(ans%i == 0)  {mi = i; break;}
            }
            printf("%d %d
",ans, mi);
        }
    }
    else
    {
        memset(vis,0,sizeof(vis));
        memset(flag,0,sizeof(flag));
        for(int i=1;i<=n;i++)
        {
            if(!vis[i])
            {
                mx = mi = d[i] = 0;
                dfs2(i);
                ans += mx-mi+1;
            }
        }
        if(ans<3)  puts("-1 -1");
        else printf("%d 3
",ans);
    }
    return 0;
}