离线算法也就是需要先把所有查询给保存下来,最后一次输出结果。
离线算法是基于并查集实现的,首先就是初始化P[i] = i。
接下来对于每个点进行dfs:
①首先判断是否有与该点有关的查询,如果当前该点为u,与它有关的点为v,如果v已经访问过了,那么它们的LCA就是find(v)。如果v还没有访问,那就不用管它。
②对该点的子节点继续dfs,需要注意的是,dfs完之后需要需要p[v]=u,将v点并到其父亲节点上。
1 void LCA(int u) 2 { 3 vis[u]=1; 4 for(int i=qhead[u];i!=-1;i=query[i].next) 5 { 6 int v=query[i].v; 7 if(vis[v] && !mark[Find(v)]) //mark数组是为了针对非连通图的情况 8 ans[query[i].index]=Find(v); //index次询问的公共祖先为Find(v) 9 } 10 11 for(int i=ehead[u];i!=-1;i=e[i].next) 12 { 13 int v=e[i].v; 14 if(!vis[v]) 15 {17 LCA(v); 18 p[v]=u; 19 } 20 } 21 }
接下来详细解释一下为什么是这么一个原理:
对于任意两个节点u和v来说,它们只有两种关系:①子节点关系;②非子节点关系。
①子节点关系
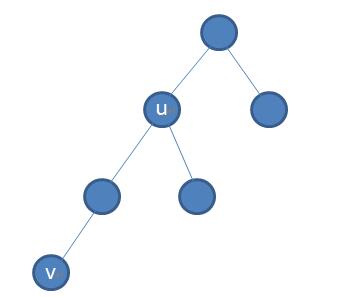
u和v的公共祖先很明显的就是u,在访问u结点的时候,v节点还没有被访问,此时继续访问u的子节点。那么当访问到v节点的时候,因为u节点已经被访问,所以此时u、v的LCA=find(u),由于此时p[u]=u,所以此时它们的LCA就是u。
②非子节点关系

此时u和v两个节点肯定有一个先访问,另一个后访问,现在就假设u先访问(v先访问的情况也是一样的)。
访问到u时,v还没有被访问,所以此时不用管,继续访问u的子节点,当u的子节点访问完之后,p[u] = f。
接下来访问到v时,由于u已经被访问,所以它们的LCA就是find(u),也就是p[f]=f,因为此时f的子节点还没有访问完,所以p[f]是不变的。
好了,两种情况都证明了。