https://vjudge.net/problem/UVA-1343
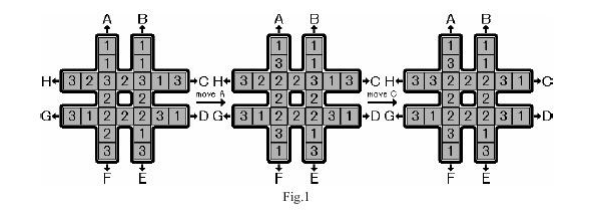
题意:如图所示,一共有8个1,8个2和8个3,如何以最少的移动来使得中间8个格子都为同一个数。
思路:状态空间搜索问题。
用IDA*算法的话会比较快,而且代码比较简洁。
IDA*的关键就是要寻找一个估价函数h(),在这道题目中,每次移动最多只会使一个格子的数字正确,所以当maxd-d<h()时便可以剪枝。
1 #include<iostream> 2 #include<string> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 7 int position[8][7] = { 8 { 0, 2, 6, 11, 15, 20, 22 }, { 1, 3, 8, 12, 17, 21, 23 }, //八个方向格子的坐标值 9 { 10, 9, 8, 7, 6, 5, 4}, { 19, 18, 17, 16, 15, 14, 13 }, 10 {23, 21, 17, 12, 8, 3, 1}, { 22, 20, 15, 11, 6, 2, 0 }, 11 {13, 14, 15, 16, 17, 18, 19}, { 4, 5, 6, 7, 8, 9, 10 } 12 }; 13 14 int goal[] = { 6, 7, 8, 11, 12, 15, 16, 17 }; //目标状态的坐标 15 16 int a[25]; 17 char order[30]; //记录路径 18 19 bool is_goal() //判断是否已达到目标状态 20 { 21 for (int i = 0; i < 7; i++) 22 { 23 if (a[goal[i]]!=a[goal[i + 1]]) return false; 24 } 25 return true; 26 } 27 28 int h() //算出不匹配的最小值 29 { 30 int n1 = 0, n2 = 0, n3 = 0; 31 for (int i = 0; i < 8; i++) 32 { 33 if (a[goal[i]] == 1) n1++; 34 else if (a[goal[i]] == 2) n2++; 35 else if (a[goal[i]] == 3) n3++; 36 } 37 return 8 -max( max(n1, n2),n3); 38 } 39 40 void rotate(int k) //往指定的方向移动 41 { 42 int temp = a[position[k][0]]; 43 for (int i = 1; i < 7; i++) 44 { 45 a[position[k][i-1]] = a[position[k][i]]; 46 } 47 a[position[k][6]] = temp; 48 } 49 50 bool dfs(int d, int maxd) 51 { 52 if (is_goal()) return true; 53 if (maxd - d < h()) return false; //剪枝 54 int old[25]; //用来保存原来的序列 55 memcpy(old, a, sizeof(a)); 56 for (int i = 0; i < 8; i++) 57 { 58 rotate(i); //往第i个方向移动 59 order[d] = i + 'A'; 60 if (dfs(d + 1, maxd)) return true; 61 memcpy(a, old, sizeof(old)); //如果失败,则恢复原来序列 62 } 63 return false; 64 } 65 66 void solve() 67 { 68 if (is_goal()) 69 { 70 cout << "No moves needed" << endl << a[6] << endl; 71 return; 72 } 73 for (int maxd = 1;; maxd++) 74 { 75 if (dfs(0, maxd)) 76 { 77 order[maxd] = '�'; 78 cout << order << endl << a[6] << endl; 79 return; 80 } 81 } 82 } 83 84 int main() 85 { 86 //freopen("D:\txt.txt", "r", stdin); 87 while (cin >> a[0] && a[0]) 88 { 89 for (int i = 1; i < 24; i++) 90 cin >> a[i]; 91 solve(); 92 } 93 return 0; 94 }