李宏毅机器学习HW1（梯度下降）

问题引入

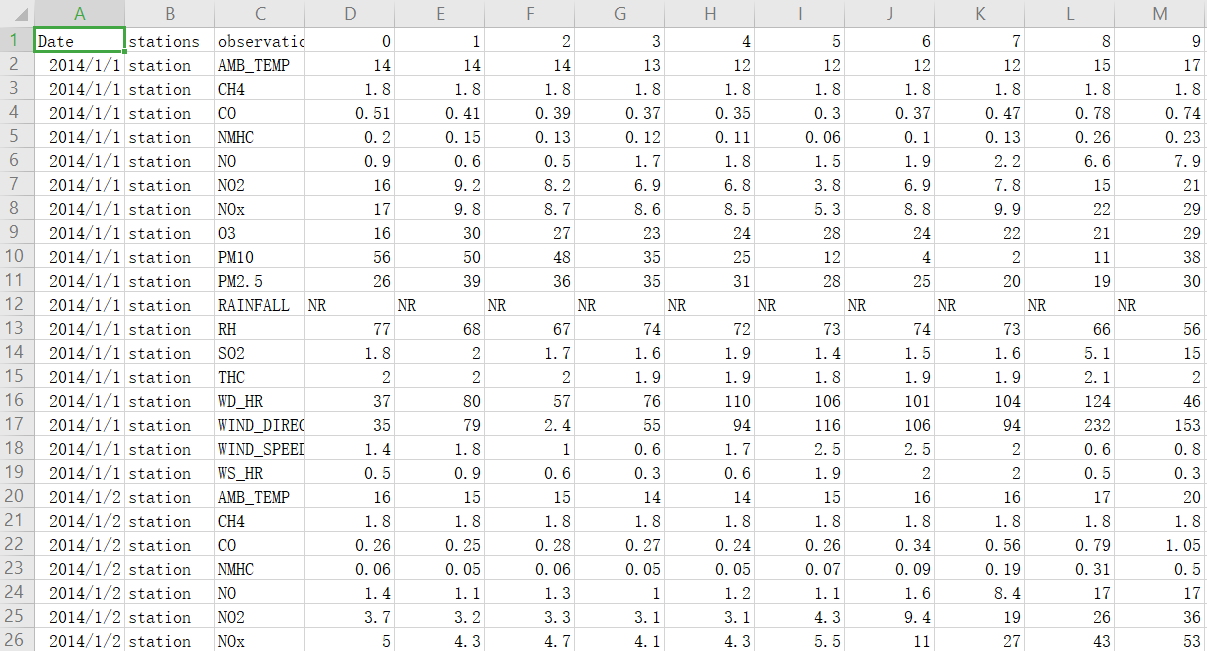
作业所给的数据是某地的观测记录，每个月取前20天的数据，观测数据共有18个指标，每小时记录这18个指标的值，共记录12个月。

现在从剩下的资料中取出连续的9小时的观测数据，请预测第10个小时的PM2.5指标的值。

数据处理

先将csv文件内容读入进来，首先需要注意的是RAINFALL指标还有NR，得把它替换成0。

def read_csv():
     df = pd.read_csv(CSV_file_path)
     df = df.iloc[:, 3:]                    # 前面3列的内容没用
     df.replace('NR', 0, inplace=True)      # 将降雨量中的NR替换为0
     return df

接下来生成测试集，因为最后预测数据的特征是连续9小时的观测数据，所以我们每次取连续的10小时观测数据，前9小时的数据作为特征，最后一小时的PM2.5指标观测值作为标签值。

为方便生成数据，先将数据作如下处理：

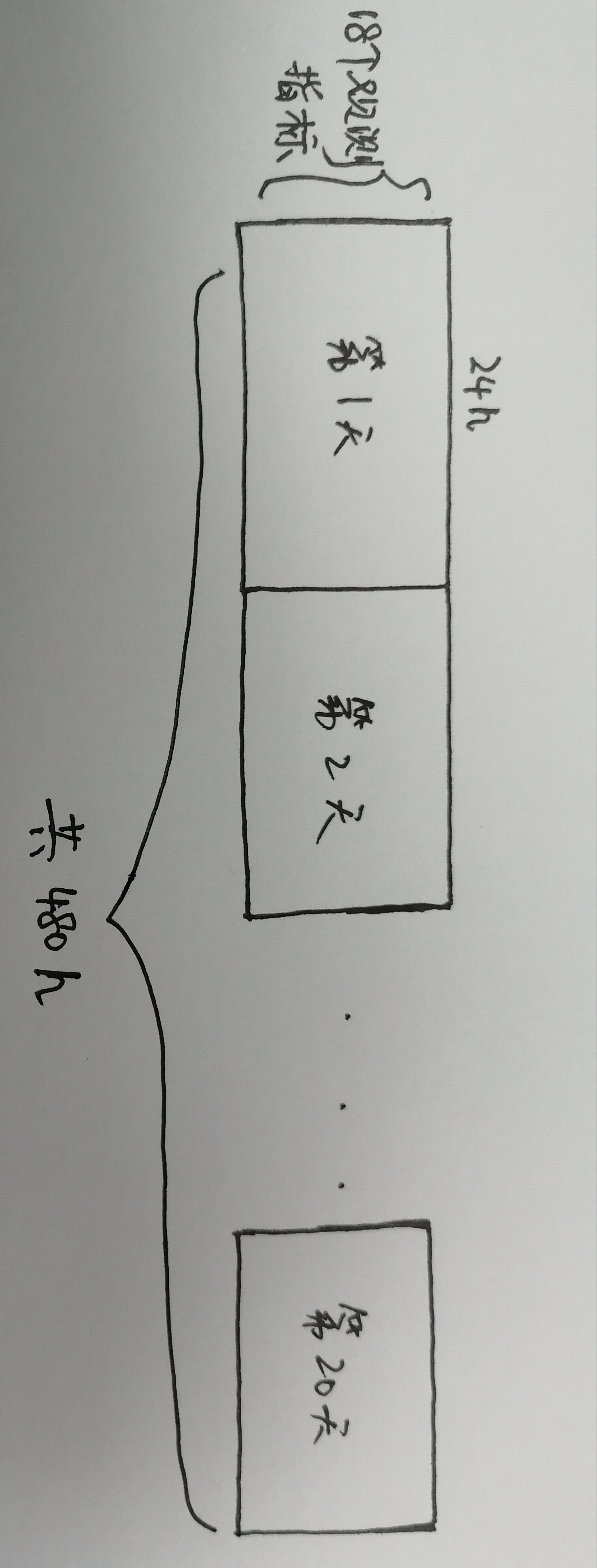
一共生成12行这样的数据，注意每个月不能连起来，因为每个月只取了前20天，并不连续。

接下来生成数据即可，代码如下：

def get_train_data(df):
    data = df.to_numpy()
    month_data = {}

    for month in range(12):
        sample = np.empty([18, 480])       # 一共18个观测指标，24*20=480
        for day in range(20):              # 将每个月的20天数据连接起来
            sample[:, day*24:(day+1)*24] = data[month*20*18+day*18:month*20*18+(day+1)*18, :]
        month_data[month] = sample

    x_set = np.empty((12*471, 18*9))       # 每10小时可取出一组数据，共471组，一共12个月，所以总的数据量为12*471，属性值一共有18*9
    y_set = np.empty((12*471, 1))

    for month in range(12):
        for day in range(20):
            for hour in range(24):
                if day == 19 and hour > 14:
                    continue
                x_set[month * 471 + day * 24 + hour, :] = month_data[month][:, day * 24 + hour: day * 24 + hour + 9].reshape(1, -1)   # 将数据　　重组成一行
                y_set[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9]   # 只取第9行的PM2.5观测值
    return x_set, y_set

为了能获得更好的效果，在梯度下降之前先进行标准化处理。

这里使用的公式为z-score 标准化：

$x_{i}^{r} = frac{x_{i}^{r}-m_{i}}{sigma_i}$

其中$x_{i}^{r} $表示第$r$组数据中的第$i$个值，$m_{i}$表示所有样本中第$i$个值的均值，$sigma_i$表示所有样本中第$i$个值的标准差。

def normalization(x_set):
    x_mean = np.mean(x_set, axis=0)
    x_std = np.std(x_set, axis=0)
    for row in range(len(x_set)):
        for col in range(len(x_set[0])):
            if x_std[col] != 0:               # 标准差为0表示数据基本无波动
                x_set[row][col] = (x_set[row][col] - x_mean[col])/x_std[col]
    return x_set, x_mean, x_std

在得到训练数据后，我们再拆分一部分数据出来作为验证集。

def split_data(x_set, y_set):
    x_train_set = x_set[: math.floor(len(x_set) * 0.8), :]
    y_train_set = y_set[: math.floor(len(y_set) * 0.8), :]
    x_validation = x_set[math.floor(len(x_set) * 0.8):, :]
    y_validation = y_set[math.floor(len(y_set) * 0.8):, :]
    return x_train_set, y_train_set, x_validation, y_validation

梯度下降

我们首先假设线性回归的函数为：

$H(x)=w_{0}+w_{1}x_{1}+w_{2}x_{2}+···+w_{n}x_{n}$

损失函数使用均方误差，李宏毅老师的示例作业里使用了均方根误差，但是代码中算梯度的式子我没看懂，还请懂的人可以告诉我下，所以这里我就用了均方误差。

$L(w)=frac{1}{2m}sum_{i=1}^{m}(H(x^{(i)})-y^{(i)})^{2}$

现在对参数$w_{j}$求偏导，即

$frac{partial L(w)}{w_{j}}=frac{1}{m}sum_{i=1}^{m}(H(x^{(i)})-y^{(i)})x_{j}^{(i)}$

这式子是可以转换成矩阵运算的，具体的请看下面的代码。

在得到梯度之后，需要不断更新$w$参数的值，在这里使用李宏毅老师所讲的Adagrad方法，公式为：

$w^{t+1} = w^{t}-frac{eta^{t}}{sigma^{t}}g^{t}$

其中$eta^{t}=frac{eta}{sqrt{t+1}}$，这可以使得我们一开始以尽量快得到速度靠近目标，然后逐渐减小学习率，$g^{t}=frac{partial L(w)}{w}$，$sigma^{t}=sqrt{frac{1}{t+1}sum_{i=0}^{t}(g^{i})^2}$。

经过化简计算，即为：

$w^{t+1} = w^{t}-frac{eta}{sqrt{sum_{i=0}^{t}(g^{i})^2}}g^{t}$

def training(x_train_set, y_train_set):
    dim = 18 * 9 + 1      # w参数的维度，+1是可以把b也当成一个w
    w = np.ones([dim, 1])
    b = np.ones([len(x_train_set), 1])
    x = np.concatenate((b, x_train_set), axis=1).astype(float)  # 将b初始化为1，加载样本属性值的最前面

    learning_rate = 100      # 学习率
    iter_time = 20000        # 迭代次数
    adagrad = np.zeros([dim, 1])
    eps = 0.0000000001       # 新的学习率是learning_rate/sqrt(sum_of_pre_grads**2),而adagrad=sum_of_grads**2,所以处在分母上而迭代时adagrad可能为0，所以加上一个极小数，使其不除0

    for i in range(iter_time):
        loss = np.sum(np.power(np.dot(x, w) - y_train_set, 2)) / len(x_train_set)/2    # 均方误差
        if i % 100 == 0:                                                               # 每迭代100次输出loss值
            print(str(i)+':'+str(loss))
        gradient = np.dot(x.T, np.dot(x, w) - y_train_set)/len(x_train_set)            # 计算梯度
        adagrad += gradient ** 2                                                       # 累加adagrad值
        w = w - learning_rate * gradient / np.sqrt(adagrad+eps)                        # 更新参数
    return w

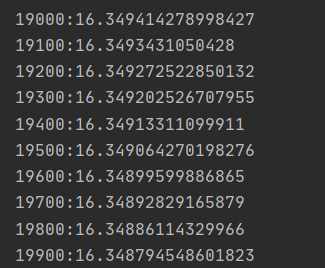
验证预测

将训练得到的$w$参数在之前拆分得到的验证集上进行计算。

def validation(w, x_validation, y_validation):
    b = np.ones([len(x_validation), 1])
    x = np.concatenate((b, x_validation), axis=1).astype(float)
    loss = np.sum(np.power(np.dot(x, w) - y_validation, 2)) / len(x_validation)/2
    print('验证的loss为' + str(loss))

最后进行预测，读入test.csv文件，也和训练数据一样，先处理一下数据，然后直接np.dot(x,w)即可。

def predict(w, x_mean, x_std):
    df = pd.read_csv(test_file_path, header=None)
    df = df.iloc[:, 2:]
    df.replace('NR', 0, inplace=True)
    data = df.to_numpy()
    pre_data = np.empty((240, 18*9))
    for i in range(240):
        pre_data[i, :] = data[18*i:18*(i+1), :].reshape(1, -1)
    for row in range(len(pre_data)):             # 需要标准化，而且均值和标准差需要使用之前的
        for col in range(len(pre_data[0])):
            if x_std[col] != 0:
                pre_data[row][col] = (pre_data[row][col] - x_mean[col]) / x_std[col]
    b = np.ones([len(pre_data), 1])
    pre_data = np.concatenate((b, pre_data), axis=1).astype(float)
    result = np.dot(pre_data, w)

    file = open('result.csv', 'w')
    for i in range(240):
        file.write('id_' + str(i) + ',' + str(result[i][0]))
        file.write('
')
    file.close()

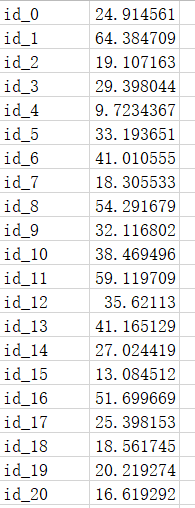
预测的结果为：

完整代码

import numpy as np
import pandas as pd
import math

CSV_file_path = './train.csv'
test_file_path = './test.csv'


def read_csv():
    df = pd.read_csv(CSV_file_path)
    df = df.iloc[:, 3:]
    df.replace('NR', 0, inplace=True)      # 将降雨量中的NR替换为0
    return df


def get_train_data(df):
    data = df.to_numpy()
    month_data = {}

    for month in range(12):
        sample = np.empty([18, 480])       # 一共18个观测指标，24*20=480
        for day in range(20):              # 将每个月的20天数据连接起来
            sample[:, day*24:(day+1)*24] = data[month*20*18+day*18:month*20*18+(day+1)*18, :]
        month_data[month] = sample

    x_set = np.empty((12*471, 18*9))       # 每10小时可取出一组数据，共471组，一共12个月，所以总的数据量为12*471，属性值一共有18*9
    y_set = np.empty((12*471, 1))

    for month in range(12):
        for day in range(20):
            for hour in range(24):
                if day == 19 and hour > 14:
                    continue
                x_set[month * 471 + day * 24 + hour, :] = month_data[month][:, day * 24 + hour: day * 24 + hour + 9].reshape(1, -1)   # 将数据重组成一行
                y_set[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9]   # 只取第9行的PM2.5观测值
    return x_set, y_set


def normalization(x_set):
    x_mean = np.mean(x_set, axis=0)
    x_std = np.std(x_set, axis=0)
    for row in range(len(x_set)):
        for col in range(len(x_set[0])):
            if x_std[col] != 0:               # 标准差为0表示数据基本无波动
                x_set[row][col] = (x_set[row][col] - x_mean[col])/x_std[col]
    return x_set, x_mean, x_std


def split_data(x_set, y_set):
    x_train_set = x_set[: math.floor(len(x_set) * 0.8), :]
    y_train_set = y_set[: math.floor(len(y_set) * 0.8), :]
    x_validation = x_set[math.floor(len(x_set) * 0.8):, :]
    y_validation = y_set[math.floor(len(y_set) * 0.8):, :]
    return x_train_set, y_train_set, x_validation, y_validation


def training(x_train_set, y_train_set):
    dim = 18 * 9 + 1      # w参数的维度，+1是可以把b也当成一个w
    w = np.ones([dim, 1])
    b = np.ones([len(x_train_set), 1])
    x = np.concatenate((b, x_train_set), axis=1).astype(float)  # 将b初始化为1，加载样本属性值的最前面

    learning_rate = 100      # 学习率
    iter_time = 20000        # 迭代次数
    adagrad = np.zeros([dim, 1])
    eps = 0.0000000001       # 新的学习率是learning_rate/sqrt(sum_of_pre_grads**2),而adagrad=sum_of_grads**2,所以处在分母上而迭代时adagrad可能为0，所以加上一个极小数，使其不除0

    for i in range(iter_time):
        loss = np.sum(np.power(np.dot(x, w) - y_train_set, 2)) / len(x_train_set)/2    # 均方误差
        if i % 100 == 0:                                                               # 每迭代100次输出loss值
            print(str(i)+':'+str(loss))
        gradient = np.dot(x.T, np.dot(x, w) - y_train_set)/len(x_train_set)            # 计算梯度
        adagrad += gradient ** 2                                                       # 累加adagrad值
        w = w - learning_rate * gradient / np.sqrt(adagrad+eps)                        # 更新参数
    return w


def validation(w, x_validation, y_validation):
    b = np.ones([len(x_validation), 1])
    x = np.concatenate((b, x_validation), axis=1).astype(float)
    loss = np.sum(np.power(np.dot(x, w) - y_validation, 2)) / len(x_validation)/2
    print('验证的loss为' + str(loss))


def predict(w, x_mean, x_std):
    df = pd.read_csv(test_file_path, header=None)
    df = df.iloc[:, 2:]
    df.replace('NR', 0, inplace=True)
    data = df.to_numpy()
    pre_data = np.empty((240, 18*9))
    for i in range(240):
        pre_data[i, :] = data[18*i:18*(i+1), :].reshape(1, -1)
    for row in range(len(pre_data)):             # 需要标准化，而且均值和标准差需要使用之前的
        for col in range(len(pre_data[0])):
            if x_std[col] != 0:
                pre_data[row][col] = (pre_data[row][col] - x_mean[col]) / x_std[col]
    b = np.ones([len(pre_data), 1])
    pre_data = np.concatenate((b, pre_data), axis=1).astype(float)
    result = np.dot(pre_data, w)

    file = open('result.csv', 'w')
    for i in range(240):
        file.write('id_' + str(i) + ',' + str(result[i][0]))
        file.write('
')
    file.close()


if __name__ == '__main__':
    df = read_csv()
    x_set, y_set = get_train_data(df)
    x_set, x_mean, x_std = normalization(x_set)
    x_train_set, y_train_set, x_validation, y_validation = split_data(x_set, y_set)
    w = training(x_train_set, y_train_set)
    validation(w, x_validation, y_validation)
    predict(w, x_mean, x_std)