监督学习(supervised learning):有一个监督者来判断学习结果是否正确,即类似在样本训练中给所有的样本加上标签label,如果判断结果和标签相符合就不作改变,否则改变相应的参数。
非监督学习:显然是无对错信息的一种学习过程,在这个过程中机器自己学会对不同的输入进行聚类,没有标签。
强化学习:(以后再写)
神经网络介绍:
现在几乎所有事物我们都可以进行量化用数字来表示,比如一个图片(RGB三通道),它的每个像素有三个数值代表红绿蓝三种颜色的深浅,许多这样的像素按照对应的顺序就构成了一张图片; 声音是一个随时间变化的波,我们可以检测到其振幅和音调等,在时间上可以选取每个时刻都用数字刻画对应的声音;判断一个人的健康状况我们可以通过体检单上的各种检测数据来判断,医生也是要根据图像(ct, X-ray)和数据(体检单,阳性阴性血压血糖等)来判断一个人是否有相关的疾病;可以看到好多事物的属性都可以用数据量化来表示我们经常遇到的这些问题也可以用数据去描述。
Neural Network 示意小图:
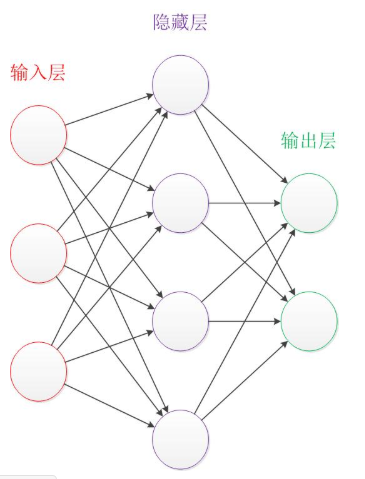
输入层,隐藏层,和输出层是其主要构成(最简单的结构)
我们的输入就是量化成了一系列数字,这个数据通过输入层输入(一个输入层的神经元接受一个数字)然后经过一些函数的计算和判断产生一个输出,输出给下一层的所有神经元,但是并不一定全都作用于下一层所有的神经元,因为在传递的过程中还有一个叫做权重的东西。(在图中的边上,也就是带有箭头的线上),每一个上层神经元的输出x都要乘上一个权重w同时可能再接受一个偏置b,才是这一层神经元的输入,(注:偏置可以单独作为一个上层中的神经元,即上一层的一个神经元是没有输入的,它直接向这一层每个神经元都传入一个偏置b,可能每个神经元接受的b是不一样的,因为每一个产生输入值的权重和偏置可以看成是这一层神经的一部分,即所有的边都属于其指向的一层,当然也可以有其他的理解。)
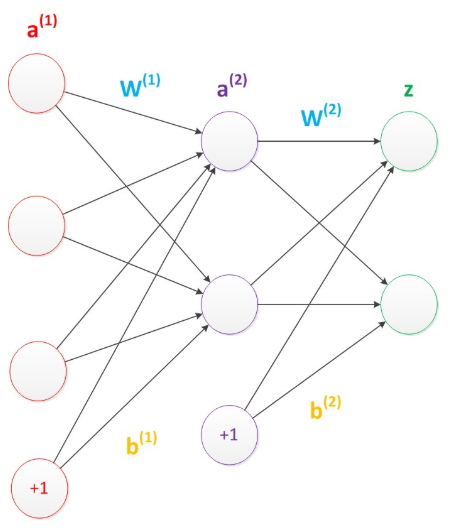
虽然每个神经元接受的数据只能经过线性计算(y = w*x + b),但是我们可以通过非线性激活函数实现非线性运算的能力。
每一层都有若干个神经元,这样每一层的所有的权重(即边上的权重参数)构成了一个矩阵:
比如这个图:
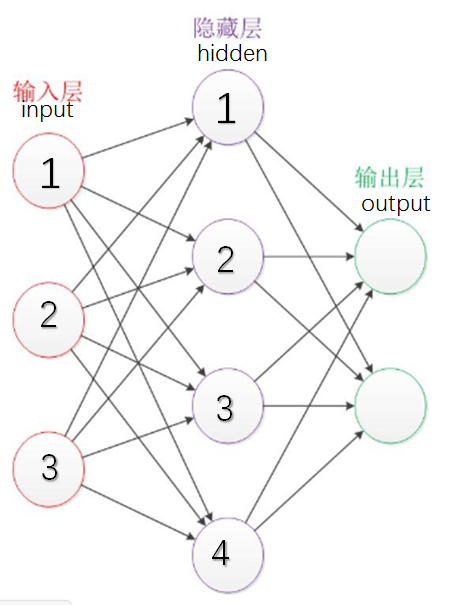
input层第i个神经元到hiddeng层第j个神经元之间的权重定为wji (注意下标的顺序),我们把每一层的上一层发出的数据out都看成一个列向量,这里以input层和hidden层举例子,input的数据向量 = X, hidden 的输入的数据向量(经过加权计算)为Y,可以看到我们我们可以把所有的wji (i>0&&i<=3, j>0&&j<=4)排列成一个4*3的矩阵,X是一个3*1的向量,Y是一个4*1的向量,我们可以看到W * X = Y,这个简单的矩阵式子就代表了两个神经层之间的参数传递(这里的W是左乘,如果我们把每一层的输入都看成行向量,那么就是用wij (同样注意一下下标的顺序)形成了一个3*4的矩阵W' 使得 X * W' = Y, (W'是W的转置)这就算出了加权之后本层神经层所接收的输入。
当然我们每一层接受的数值向量还要加上权重,在上面的例子里应当加上一个4*1 的向量B,分量依次是hidden层1,2,3,4的偏置b1, b2, b3, b4
这样就算出了hidden层,也就是本层神经元的input数据向量: Y = W * X + B; 用一个矩阵等式就可以表达。
这里根据高等代数的理解,我们通过一个或者多个矩阵进行一次或者多次线性映射,将这一个数据向量转换成另一个空间的(一般维数都有变化嘛)的基下的坐标表示,要注意仅在层之间通过矩阵乘法这样的线性运算是没有办法处理非线性问题的,这也是我们为什么要引入非线性激活函数的原因,我们在分类的过程中大部分问题可能都涉及到非线性的分类,那么引入非线性激活函数就可以保证非线性运算,同时输入的维度其实可以代表不同属性对应的参数,也就是不同神经元的信息,比如一个人的身高,肤色(用数字量化),体重,这种,矩阵的乘法是一种线性变换,变成其他维度向量可以增多或是减少要考虑的属性或者数据信息。这样计算机就可以通过简单的逻辑电路完成对应的判断了。(这个只是个人想法)
同时不同的权重对应的是对数据的分重点性判断,可以理解为每一层的一个神经元可能只判断一个细节(比如一个人有没有眼睫毛)那么它接受的上一层的输出时对应分配的权重就应该在眼睛附近的数据更大,其他地方接近零,通过加权就可以将一个数据向量分成不同的细节交给不同的神经元处理,一个神经元完成一件小任务,就像电路中的一个逻辑门,众多逻辑门放在一起就可以完成复杂的运算和判断。