对于一个线性空间U到线性空间V的映射, 可以取定U的一个基α1,α2——αn,由于U中每一个向量都可以由U的基线性表出,那么V中每一个对应U中一个向量α的象β就一定可以由U的基的象的线性组合表出,那么一个映射就完全由它原空间的一个基的象确定,我们在用矩阵表示线性映射的时候其实是选定了U的一组基,然后将U的每个基向量的象用V中基向量来线性表出,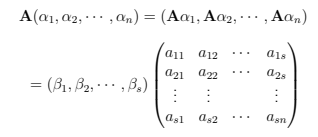
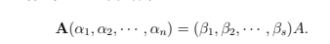
这里线性映射是从一个向量到另一个向量,这里的向量是广义的,只要在线性空间里的元素就可以是向量,(比如可以是一个数字,一个矢量,也可以是一个矩阵,)一定要注意的一点是,一个线性映射对应的矩阵是由选取的U和V的基所决定的,也就是说映射对应的矩阵其实应该是两个不同空间的基的对应关系,如果有基的变换那么对应的矩阵也要进行变换。
由于空间里的向量可以用选定的基向量和在这个基下的坐标确定(我们在这里将向量量化了,即赋予坐标以实际意义),那么U中向量α的坐标便代表了在U中表示这个向量的线性组合,如此由上面矩阵的定义可以清楚,用映射对应的矩阵右乘一个坐标x1的列向量就可以把这个线性组合对应到V的基向量上,也就是我们如果用另一个在V中的坐标x2表示α的象β,那么Ax1=x2,A是这个线性映射对应的矩阵,即我们都用坐标来表示向量的话,矩阵告诉我们怎样转换可以将U中α的坐标变成映射之后V中β的坐标。(这也是两个基用行向量来表示基向量组然后右乘矩阵得到另一个基向量组的原因,不可以把左乘右乘搞混)
若(α1, α2,·····, αn)S=(γ1,γ2·····,γn)为U中基的变换,(β1,β2,····,βm)Q=(δ1,δ2,·······,δm),
则变换两个空间的基之后映射A所对应的矩阵就是Q^-1·A·S,(自己做一下推导就可以得出)。
由于一个映射完全由它的原象空间的基的象决定,那么线性映射是将一个线性空间变成另一个线性空间,但是这种映射可能使线性空间降维,不可能升维,因为原象空间的基的数目确定了,无法升维。
在这里的线性映射是两个空间之间的,那么一个空间到它自己本身的映射(线性变换)又是什么样的呢?
由上可以猜测就是S^-1*A*S
今天看过一些视频再记录一下比较便于理解线性映射的解释:
像上述映射在基的变换下看似十分不同,但是应该看到基的变换其实应该是用不同的坐标来表示一个线性空间中相同的向量,那么在这里就可以看到对于一个坐标X=(x1,x2,……,xn)^T, 一个基α=(α1, α2,·····, αn)下表示的向量就是αX ,(就是基的线性组合),但是我们如果要用另一个基γ=(γ1,γ2·····,γn)=(α1, α2,·····, αn)S来表示同一个向量的话,坐标Y(γ下)满足这样的关系γY=αSY=αX, 可以看到X=SY, 那么S的作用就是把在γ基下的坐标翻译为在α基下的坐标(因为总有一些坐标系的基非常便于表示任何一个向量而且计算比较容易,没错我觉得就是正交基,非常亲切自然,,,,),那么线性映射中不同基的变换下的映射所对应的矩阵的变换Q^-1·A·S的解释可以是这样的:对于任何一个坐标X(基变换之后),我们先左乘S,SX就是我们可以确定的映射A(这是我们已经确定的,知道原象和象空间的基和映射的矩阵)对应的U中的坐标(翻译成A可以接受的向量坐标,因为A接受的向量的基是变换之前的α)这样再进行A这个映射的到没有对象变换基之前的在象对应空间里的坐标ASX,这个坐标是A直接产生的象的坐标,它的基是β=(β1,β2,····,βm),我们不知道这个象在δ=(δ1,δ2,·······,δm)下的坐标,那怎么办呢?我们可以把δ下的坐标左乘Q翻译成β下的坐标,那么反过来就要对β下的坐标左乘Q^-1翻译成δ下的坐标,这样就是Q^-1* A *S 就是把一个在γ下的坐标表示的向量映射到δ下的坐标所对应的这个映射(映射它从来就没有变过~~)所对应的矩阵。
至于线性变换中的基,线性变换映射前后所对应的都是一个基,所以就没有像从一个空间到另一个空间的映射那么复杂。