Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k ≥ 1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a1, a2, ..., ak and b1, b2, ..., bk satisfying the following requirements:
- k ≥ 1
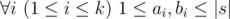
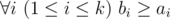
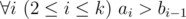
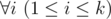 t is a substring of string saisai + 1... sbi (string s is considered as 1-indexed).
t is a substring of string saisai + 1... sbi (string s is considered as 1-indexed).
As the number of ways can be rather large print it modulo 109 + 7.
Input consists of two lines containing strings s and t (1 ≤ |s|, |t| ≤ 105). Each string consists of lowercase Latin letters.
Print the answer in a single line.
ababa
aba
5
题意:
给两个串S,T,问能找出多少的S的(a1,b1)(a2,b2)..(ak,bk),使Sa1---Sb1,...Sak---Sbk都包含子串T,其中k>=1,且(a1,b1)...(ak,bk)互不相交。
题解:
kmp预处理匹配点。。。
f[i]表示前i个的合法划分数。。
f[i]=f[i–1] (表示将最后一个舍弃)
sum[i]=∑ f[k] (k<=i)
设上一个匹配点为last
f[i]+=sum[last–1]+last
即有两种情况
[1….L-1(这部分任意,只要合法,允许舍弃末尾)] [L…i] 这样划分
或者直接 k=1 即只有一个划分[L…i]
L<=last
#include <iostream> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include<vector> using namespace std; const int N = 1e5+20, M = 30005, mod = 1000000007, inf = 0x3f3f3f3f; typedef long long ll; //不同为1,相同为0 ll next[N],dp[N],f[N],sum[N]; char s[N],t[N]; int main() { scanf("%s%s",t+1,s+1); int n = strlen(t+1),m = strlen(s+1); int k = 0; for(int i=2;i<=m;i++) { while(k>0&&s[k+1]!=s[i]) k = next[k]; if(s[k+1]==s[i])k++; next[i] = k; } k = 0; for(int i=1;i<=n;i++) { while(k>0&&s[k+1]!=t[i]) k = next[k]; if(s[k+1]==t[i]) k++; if(k==m) k = next[k],f[i] = 1; } int last = -1; for(int i=1;i<=n;i++) { dp[i] = dp[i-1]; if(f[i]) last = i-m+1; if(last!=-1) dp[i]+=sum[last-1]+last; sum[i] = sum[i-1]+dp[i]; dp[i]%=mod,sum[i]%=mod; } cout<<dp[n]<<endl; }