B. The Child and Zoo
Description
Of course our child likes walking in a zoo. The zoo has n areas, that are numbered from 1 to n. The i-th area contains ai animals in it. Also there are m roads in the zoo, and each road connects two distinct areas. Naturally the zoo is connected, so you can reach any area of the zoo from any other area using the roads.
Our child is very smart. Imagine the child want to go from area p to area q. Firstly he considers all the simple routes from p to q. For each route the child writes down the number, that is equal to the minimum number of animals among the route areas. Let's denote the largest of the written numbers as f(p, q). Finally, the child chooses one of the routes for which he writes down the value f(p, q).
After the child has visited the zoo, he thinks about the question: what is the average value of f(p, q) for all pairs p, q (p ≠ q)? Can you answer his question?
Input
The first line contains two integers n and m (2 ≤ n ≤ 105; 0 ≤ m ≤ 105). The second line contains n integers: a1, a2, ..., an (0 ≤ ai ≤ 105). Then follow m lines, each line contains two integers xi and yi (1 ≤ xi, yi ≤ n; xi ≠ yi), denoting the road between areas xi and yi.
All roads are bidirectional, each pair of areas is connected by at most one road.
Output
Output a real number — the value of 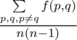 .
.
The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 4.
Sample Input
4 3
10 20 30 40
1 3
2 3
4 3
Sample Output
16.666667
HINT
题意
给你一个图
然后f(p,q)表示从p到q的所有路径中,最小价值是多少
然后让你求sigma(p,q,p!=q)f(p,q) /n*(n-1)
题解:
并查集
从大往小考虑,然后加进这个图里面,在不断加点的过程中,新加入的点一定是最小的点,于是新产生的路径,这些路径的权值,就是这个点的权值
所以并查集跑一发就好啦,维护并查集的时候,顺便维护一下每个集合的个数就好了

///1085422276 #include<bits/stdc++.h> using namespace std ; typedef long long ll; #define mem(a) memset(a,0,sizeof(a)) #define meminf(a) memset(a,127,sizeof(a)); #define inf 1000000007 #define mod 1000000007 inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1;ch=getchar(); } while(ch>='0'&&ch<='9'){ x=x*10+ch-'0';ch=getchar(); }return x*f; } //************************************************ const int maxn=100000+5; int parent[maxn],a[maxn],n,m,num[maxn]; int finds(int x){ if(x==parent[x])return x; return parent[x]=finds(parent[x]); } struct ss { int u,v,w; }e[maxn]; int cmp(ss s1,ss s2){ return s1.w>s2.w; } int main() { n=read(),m=read(); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } for(int i=1;i<=n;i++){ parent[i]=i;num[i]=1; }int u,v; for(int i=1;i<=m;i++){ scanf("%d%d",&u,&v); e[i].u=u; e[i].v=v; e[i].w=min(a[u],a[v]); } sort(e+1,e+m+1,cmp); double A=0; for(int i=1;i<=m;i++){ int fx=finds(e[i].u); int fy=finds(e[i].v); if(fx!=fy){ A+=1.0*num[fx]*num[fy]* e[i].w; parent[fy]=fx; num[fx]+=num[fy]; } } double tmp; tmp=(double )A*1.0/(n*1.0*(n-1)); printf("%.12f ",tmp*2.0); return 0; }
