分类与监督学习，朴素贝叶斯分类算法

1.理解分类与监督学习、聚类与无监督学习。

简述分类与聚类的联系与区别。

分类：找出描述并区分数据类或概念的模型，以便能够使用模型预测类标记未知的对象类。分类的目的是把数据项映射到给定的类别的某一个类中。

聚类：将本身没有类别的样本聚集成不同的组，把这组数据对象的集合叫簇。目的是使得属于同一个簇的样本之间应该彼此相似，而不同簇的样本应该足够不相似。

简述什么是监督学习与无监督学习。

监督学习：针对的是有标签的数据集，对具有概念标记的训练样本进行学习，以尽可能对训练样本集外的数据进行标记预测。

无监督学习：针对的是没有标签的数据集，对没有概念标记的训练样本进行学习，以发现训练样本集中的结构性知识。

2.朴素贝叶斯分类算法 实例

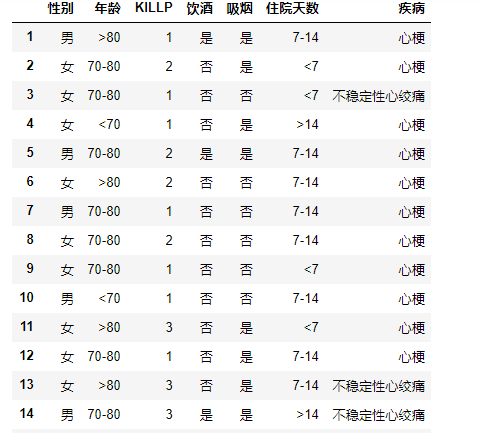
利用关于心脏情患者的临床数据集，建立朴素贝叶斯分类模型。

有六个分类变量(分类因子)：性别，年龄、KILLP评分、饮酒、吸烟、住院天数

目标分类变量疾病：–心梗–不稳定性心绞痛

新的实例：–(性别=‘男’，年龄<70, KILLP=‘I'，饮酒=‘是’，吸烟≈‘是”，住院天数<7)

最可能是哪个疾病？

上传演算过程。

假设患有心梗为事件A，患有心绞痛为事件B。性别为男为x1,年龄<70为x2,KILLP=1为x3,饮酒为x4,吸烟为x5,住院<7为x6.
p(x1|A)=7/16 P(X2|A)=4/16 P(X3|A)=9/16
P(X4|A)=3/16 P(X5|A)=7/16 P(X6|A)=4/16
P(X1，X2，X3，X4，X5，X6|A)=7/16*4/16*9/16*3/16*7/16*4/16=0.001262
p(X1|B)=1/4 P(X2|B)=1/4 P(X3|B)=1/4
P(X4|B)=1/4 P(X5|B)=2/4 P(X6|B)=2/4
P(X1，X2，X3，X4，X5，X6|B)=1/4*1/4*1/4*1/4*2/4*2/4=0.000977

p(A|x)=p(x|A)*P(A)/P(X)=0.001009/P(X)

P(B|X)=P(x|B)*p(B)/P(X)=0.000195/P(X)

因为分母是相同的，只要比较分子的数就行。

所以该患者的症状是患心梗的可能更大

3.编程实现朴素贝叶斯分类算法

利用训练数据集，建立分类模型。

输入待分类项，输出分类结果。

可以心脏情患者的临床数据为例，但要对数据预处理。

import numpy as np
import pandas
data=pandas.read_excel('心脏病患者临床数据.xlsx')
data
#对性别进行处理（男为0，女为1）
xingbie=[]
for i in data['性别']:
    if i =='男':
        xingbie.append(0)
    else:
        xingbie.append(1)
#对年龄段进行预处理（<70为1，70-80为2，>80为3）
ages=[]
for j in data['年龄']:
    if j =='<70':
        ages.append(1)
    elif j =='70-80':
        ages.append(2)
    else:
        ages.append(3)
#对住院天数进行处理（<70为1，7-14为2，>14为3）
days=[]
for k in data['住院天数']:
    if k=='<7':
        days.append(1)
    elif k=='7-14':
        days.append(2)
    else:
        days.append(3)
#处理后的数据
data1=data
data1['性别']=xingbie
data1['年龄']=ages
data1['住院天数']=days
#将数据转成数组
data_arr=np.array(data1)
data_arr
#利用贝叶斯算法对给定的组别进行分类
def NB(xingbie, ages, KILLP, drink, smoke, days):
    #初始化值
    x1_y1,x2_y1,x3_y1,x4_y1,x5_y1,x6_y1 = 0,0,0,0,0,0
    x1_y2,x2_y2,x3_y2,x4_y2,x5_y2,x6_y2 = 0,0,0,0,0,0
    y1 = 0
    y2 = 0
    #计算为心梗的概率
    for a in data_arr:
        if a[6]=='心梗':
            y1+=1
            if a[0]==xingbie:
                x1_y1+=1
            if a[1]==ages:
                x2_y1+=1
            if a[2]==KILLP:
                x3_y1+=1
            if a[3]==drink:
                x4_y1+=1
            if a[4]==smoke:
                x5_y1+=1
            if a[5]==days:
                x6_y1+=1
        else:#计算患有不稳定性心绞痛的概率
            y2+=1
            if a[0]==xingbie:
                x1_y2+=1
            if a[1]==ages:
                x2_y2+=1
            if a[2]==KILLP:
                x3_y2+=1
            if a[3]==drink:
                x4_y2+=1
            if a[4]==smoke:
                x5_y2+=1
            if a[5]==days:
                x6_y2+=1
    #计算每种症状在心梗下的概率
    x1_y1, x2_y1, x3_y1, x4_y1, x5_y1, x6_y1 = x1_y1/y1, x2_y1/y1, x3_y1/y1, x4_y1/y1, x5_y1/y1, x6_y1/y1
    #计算每种症状在不稳定性心绞痛的概率
    x1_y2, x2_y2, x3_y2, x4_y2, x5_y2, x6_y2 = x1_y2/y2, x2_y2/y2, x3_y2/y2, x4_y2/y2, x5_y2/y2, x6_y2/y2
    #多个症状在心梗下的概率
    x_y1 = x1_y1 * x2_y1 * x3_y1 * x4_y1 * x5_y1 * x6_y1
    #多个症状在不稳定性心绞痛下的概率
    x_y2 = x1_y2 *  x2_y2 * x3_y2 * x4_y2 * x5_y2 * x6_y2
    ##初始化各个特征x的值
    x1,x2,x3,x4,x5,x6=0,0,0,0,0,0
    for a in data_arr:
        if a[0]==xingbie:
            x1+=1
        if a[1]==ages:
            x2+=1
        if a[2]==KILLP:
            x3+=1
        if a[3]==drink:
            x4+=1
        if a[4]==smoke:
            x5+=1
        if a[5]==days:
            x6+=1
    lens = len(data_arr)
    #所有x的可能性
    x = x1/lens * x2/lens * x3/lens * x4/lens * x5/lens* x6/lens
    # 分别计算心梗和不稳定性心绞痛的概率
    y1_x = (x_y1)*(y1/lens)/x
    print(y1_x)
    y2_x = (x_y2)*(y2/lens)/x
    print(y2_x)
    # 判断是哪中疾病的可能更大
    if y1_x > y2_x:
        print('病人患心梗的可能更大，可能性为：',y1_x)
    else:
        print('病人患不稳定性心绞痛的可能更大，可能性为：',y2_x)

# 判断：性别=‘男’，年龄<70, KILLP=1，饮酒=‘是’，吸烟=‘是”，住院天数<7
NB(0,1,1,'是','是',1)