概念
统计语言模型是NLP的基础,是描述自然语言内在的规律的数学模型。广泛应用于各种自然语言处理问题,如语音识别、机器翻译、分词、词性标注等。
简单地说,统计语言模型就是给定一个句子W(由多个单词w1,w2,w3...组成),计算该句子可信(合理)的概率的模型,即(P(W)=P(w_1,w_2,w_3....w_n))。
概率论
联合概率
多个条件同时成立的概率,记为(P(X=a,Y=b),P(a,b),P(ab),P(a∩b))。
边缘概率
根据联合概率,保留某个变量,对其他变量进行求和/积分。
条件概率
在某个事件条件成立下,另一个事件的概率,记为(P(X=a|Y=b)=P(X=a,Y=b)/P(Y=b))。
贝叶斯公式
(P(A|B)=P(AB)/P(B)=P(B|A)*P(A)/P(B))。
其中P(A)叫做先验概率,P(A|B)叫做后验概率。
根据贝叶斯公式,就可以将一个联合概率表示为一连串条件概率的乘积,这大概就是cs224n第二节突然出现的那个公式的来源。
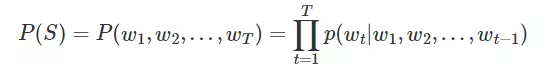
比如(P(w_1,w_2,w_3)=P(w_1)*P(w_2|w_1)*P(w_3|w_1,w_2)),把前t-1项的乘积((P(w_1,w_2,...,w_{t-1})))除过去,其实就是条件概率的表达式。
多变量条件概率的推导
根据不同情况选择不同的分解方式。
(P(X=a,Y=b|Z=c)=P(X=a,Y=b,Z=c)/P(Z=c)=P(X=a|Y=b,Z=c)*P(Y=b,Z=c)/P(Z=c))
(P(X=a|Y=b,Z=c)=P(X=a,Y=b,Z=c)/P(Y=b,Z=c)=P(X=a,Z=c|Y=b)*P(Y=b)/P(Z=c))
例子:
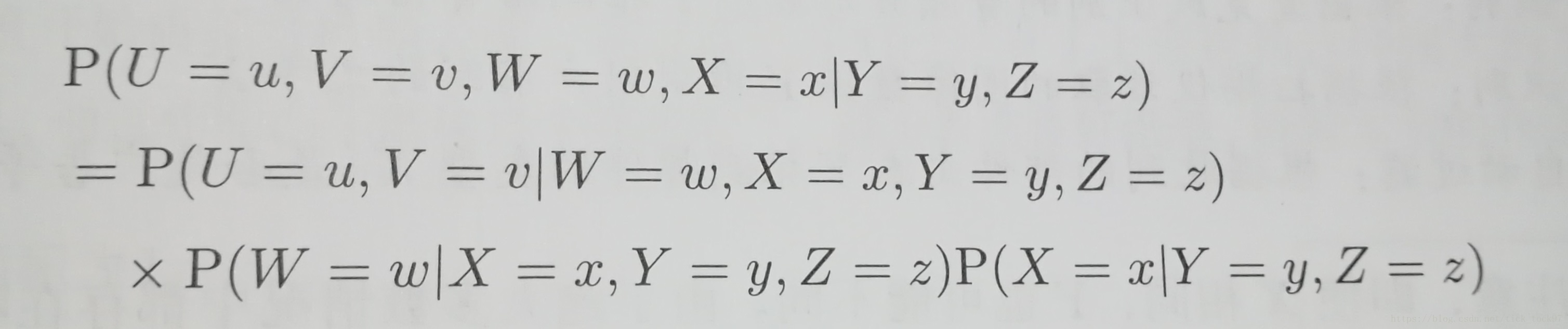
模型
unigram
假设组成句子的词与词之间相互独立,所以(P(W)=P(w_1)*P(w_2)*...*P(w_n)),这种方法简单粗暴,计算简单,但效果显然会很差。
n-gram(马尔科夫假设)
假设每个词出现的概率只与其前面n-1个词有关,也就是将模型简化为
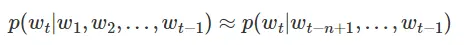
所以问题就是转化为如何去求解(P(w_t|w_{t-n+1},...,w_{t-1}))这些参数。
模型中的n一般取2或者3,因为对于每个(n个连续单词组成)这种结构,如果有N个单词,就一共有N2或者N3种组合,也就是要求出这么多的参数。
统计方法计算
比如对于n=2,根据大数定律(频率约等于概率?),(P(w_i|w_{i-1})=P(w_i,w_{i-1})/P(w_{i-1})=C(w_i,w_{i-1})/C(w_{i-1})),其中(C(w_i,w_{i-1}))表示前一个词是(w_{i-1})后一个词是(w_i)的组合在文本中出现的次数,(C(w_{i-1}))表示词(w_{i-1})在文本中出现的次数,用频率来代表概率。
这样子根据数学统计的方式得到各个参数,就能使用该模型来计算一个句子的概率,判断句子是否合理。
这种计算方法会出现零概率的问题,需要进行平滑化处理,简单的平滑化处理有Laplace平滑(Add-One平滑)和Add-k平滑。
假设文本中不同单词个数为V。
- Laplace平滑: 对于每个频率,分子+1,分母+V。
- Add-k平滑: 分子+k,分母+kV,k可以根据效果自行调整。
- backoff: 如果没有对应的n元统计值,比如(C(w_i,w_{i-1})),那就用低阶的n-1元统计值来代替,再乘以一个参数。
- Good-Turing: 略。
- 插值: 略。
参考博客
在计算时,通常会对P(W)取对数,可以防止溢出,且将概率的乘法转化为对数的加法,方便计算。
Python实现
'''
Statistical Language Model
'''
from collections import Counter
import numpy as np
import pandas as pd
from math import log2
# 语料文本
corpus = '''她的菜很好 她的菜很香 她的他很好 他的菜很香 他的她很好
很香的菜 很好的她 很菜的他 她的好 菜的香 他的菜 她很好 他很菜 菜很好'''.split()
cnt=Counter()
for sen in corpus:
for w in sen:
cnt[w]+=1
# Counter对象转tuple list
cnt=cnt.most_common()
v=len(cnt)
# 离散化+双向映射
id2word={i:cnt[i][0] for i in range(v)}
word2id={cnt[i][0]:i for i in range(v)}
print(pd.DataFrame(cnt,None,['word','freq']))
# 2-gram模型
ci=np.array([float(c[1]) for c in cnt])
ci/=ci.sum()
cij=np.zeros((v,v))+1e-8
for sen in corpus:
sen=[word2id[w] for w in sen]
for i in range(1,len(sen)):
cij[sen[i-1]][sen[i]]+=1
for i in range(v):
cij[i]=(cij[i]+1)/(cij[i].sum()+v)
words=[c[0] for c in cnt]
print(pd.DataFrame(ci.reshape(1,v),['频数'],words))
print(pd.DataFrame(cij,words,words))
# 计算句子概率
def prob(sen):
s=[word2id[w] for w in sen]
siz=len(s)
if siz==1:
return log2(ci[s[0]])
p=0
for i in range(1,siz):
p+=log2(cij[s[i-1]][s[i]])
return p
if __name__ == '__main__':
print('很好的菜', prob('很好的菜'))
print('菜很好的', prob('菜很好的'))
print('菜好的很', prob('菜好的很'))
print('他的菜很好',prob('他的菜很好')
神经网络方法
词向量 word2vec skip-gram ...