P2052 道路修建
题目描述
在 W 星球上有 n 个国家。为了各自国家的经济发展,他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬,他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用,这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如,在下图中,虚线所示道路两端分别有 2 个、4 个国家,如果该道路长度为 1,则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。 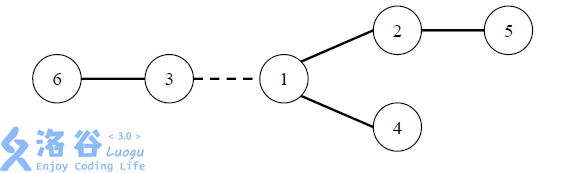
由于国家的数量十分庞大,道路的建造方案有很多种,同时每种方案的修建 费用难以用人工计算,国王们决定找人设计一个软件,对于给定的建造方案,计 算出所需要的费用。请你帮助国王们设计一个这样的软件。
输入输出格式
输入格式:
输入的第一行包含一个整数 n,表示 W 星球上的国家的数量,国家从 1 到 n 编号。 接下来 n – 1 行描述道路建设情况,其中第 i 行包含三个整数 ai、bi和 ci,表 示第 i 条双向道路修建在 ai与 bi两个国家之间,长度为 ci。
输出格式:
输出一个整数,表示修建所有道路所需要的总费用。
输入输出样例
输入样例#1:
6 1 2 1 1 3 1 1 4 2 6 3 1 5 2 1
输出样例#1:
20
说明
1≤ai, bi≤n
0≤ci≤106
2≤n≤106
pic=2603]
这个题第一眼,这是个树?好像是吧……
然后最近中了lca的毒,先dfs一下吧……
好像能在dfs过程里求出每个子数的孩子个数哎,然后好像就做出来了,迷……
然而!凡事就怕转折!!!
交到洛谷上开开心心地过了,看到讨论里有人说数据水,就到bzoj上交了一下,完美RE……
去看讨论,zyf2000说要用手工栈,蛤???这是什么鬼!!!
哦,垃圾水题浪费时间……滚去学习手工栈,然而并不太懂2333……
先贴一个非手工栈的
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int a,b; 7 long long n,c; 8 long long ans; 9 struct data{ 10 int next,to; 11 long long dis; 12 }edge[2000010]; 13 int cnt,head[1000010]; 14 long long num[1000010]; 15 //num[i]以点i为根节点的子树中的孩子个数+1(根节点) 16 bool check[1000010]; 17 void add(int start,int end,long long d){ 18 edge[++cnt].next=head[start]; 19 edge[cnt].to=end; 20 edge[cnt].dis=d; 21 head[start]=cnt; 22 } 23 int dfs(int u){ 24 num[u]=1; 25 check[u]=1; 26 for(int i=head[u];i;i=edge[i].next) 27 if(!check[edge[i].to]){ 28 dfs(edge[i].to); 29 num[u]+=num[edge[i].to]; 30 ans+=abs((n-2*num[edge[i].to])*edge[i].dis); 31 } 32 } 33 int main(){ 34 scanf("%lld",&n); 35 for(int i=1;i<n;i++){ 36 scanf("%d%d%lld",&a,&b,&c); 37 add(a,b,c); 38 add(b,a,c); 39 } 40 dfs(1); 41 printf("%lld",ans); 42 return 0; 43 }
手工栈版本的,忘敲return 0了,罪过罪过
1 //from sdfzxh 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 int n,cnt,x,y; 8 long long z,ans; 9 struct data{ 10 int nxt,to; 11 long long dis; 12 }edge[2000010]; 13 int head[1000010],stack[1000010],cur[1000010],father[1000010]; 14 long long num[1000010],mark[1000010]; 15 void add(int start,int end,long long d){ 16 edge[++cnt].nxt=head[start]; 17 edge[cnt].to=end; 18 edge[cnt].dis=d; 19 head[start]=cnt; 20 } 21 void dfs(){ 22 int top=0; 23 stack[++top]=1; 24 num[1]=1; 25 for(int i=1;i<=n;i++) cur[i]=head[i]; 26 while(top){ 27 int tmp=stack[top]; 28 while(cur[tmp]&&edge[cur[tmp]].to==father[tmp]) cur[tmp]=edge[cur[tmp]].nxt; 29 if(!cur[tmp]){ 30 top--; 31 if(father[tmp]){ 32 num[father[tmp]]+=num[tmp]; 33 ans+=abs((long long)n-2*num[tmp])*mark[tmp]; 34 } 35 continue; 36 } 37 int vt=edge[cur[tmp]].to; 38 father[vt]=tmp; 39 num[vt]=1; 40 mark[vt]=edge[cur[tmp]].dis; 41 stack[++top]=vt; 42 cur[tmp]=edge[cur[tmp]].nxt; 43 } 44 } 45 int main(){ 46 scanf("%d",&n); 47 for(int i=1;i<n;i++){ 48 scanf("%d%d%lld",&x,&y,&z); 49 add(x,y,z); 50 add(y,x,z); 51 } 52 dfs(); 53 printf("%lld",ans); 54 }