chapter 3 几何表示和变换
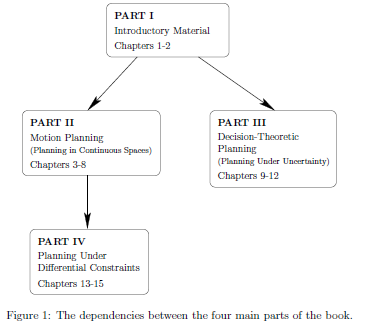
P.S: 总算到了 motion planning 部分了
几何建模
几何建模主要有两类方法:边界表示法和实体表示法。
环境模型可以是二维或三维,实体主要包括障碍物和机器人。
多边形和多面体模型
凸边形定义:子集 $ X subset mathbb{R}^{n} $ 为凸集,当且仅当, X 中任意两点连线上的所有点也属于 X 。
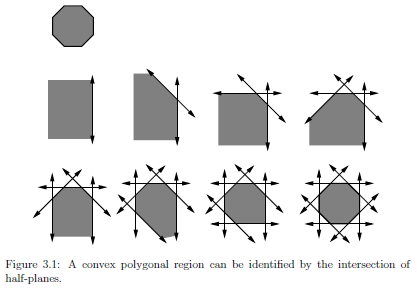
边界表示法可以用多边形表示,用一系列的边界点(left ( x_{1}, y_{1} ight ),left ( x_{2}, y_{2} ight ),cdots ,left ( x_{m}, y_{m} ight ))表示。实体表示法可以用半平面的交集表示。
半平面可以表示如下:
(H_{i} = left { left ( x,y
ight )in W| f_{i}left ( x,y
ight )leqslant 0
ight }.)
刚体变换
2D 变换
旋转:
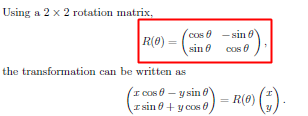
旋转 + 移动:

3D 变换
yaw, pitch, roll:

旋转变换:

反解旋转角:

利用 atan2 可以得到:
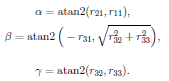
均质变换矩阵(The homogeneous transformation matrix):

刚体运动链的变化
相互依附的刚体的变化更加复杂,一系列依附的刚体被称为联动,如果刚体通过单链关联,这种联动是运动链。
2D 运动链的均质变换:

3D 运动链的均质变换:
图示:
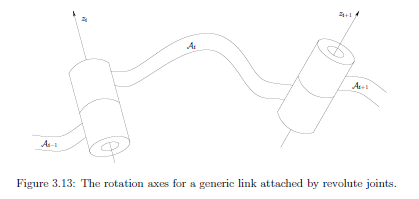
均质变换矩阵:

均质变换矩阵的 DH 参数
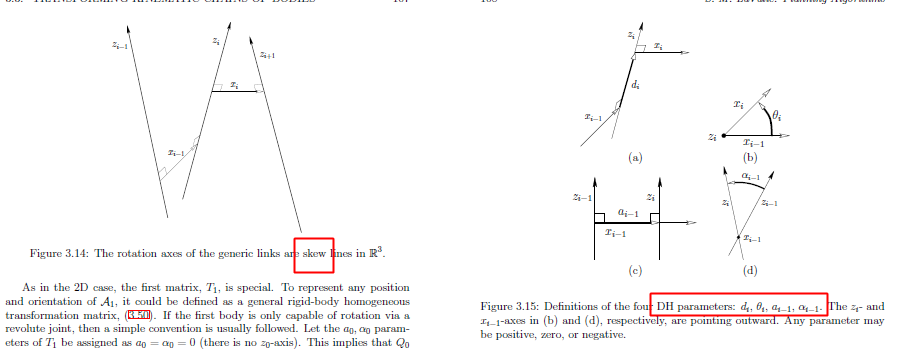
非刚体变换
线性变换:
旋转变换是一种特殊的线性变换。
同比例放大缩小:
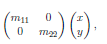
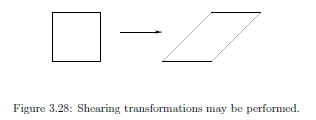
剪切变换:
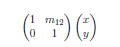
当 m12 = 1 时,剪切变换效果如下图: