题意
$n$个节点的树,每个点有权值,支持三种操作
1、 换根
2、把$x$到$y$路径上节点权值变为$z$
3、询问路径最小值
Sol
啥?你说这是TopTree的裸题?那你写去啊
很显然,如果没有第一个操作就是树剖的裸题
其实有了第一个操作也是树剖的裸题
我们考虑换根之后会对那些节点产生影响
以下图片来自(https://blog.csdn.net/lcomyn/article/details/45718295)
第一种情况:x == root
很显然直接查询子树的最小值就行
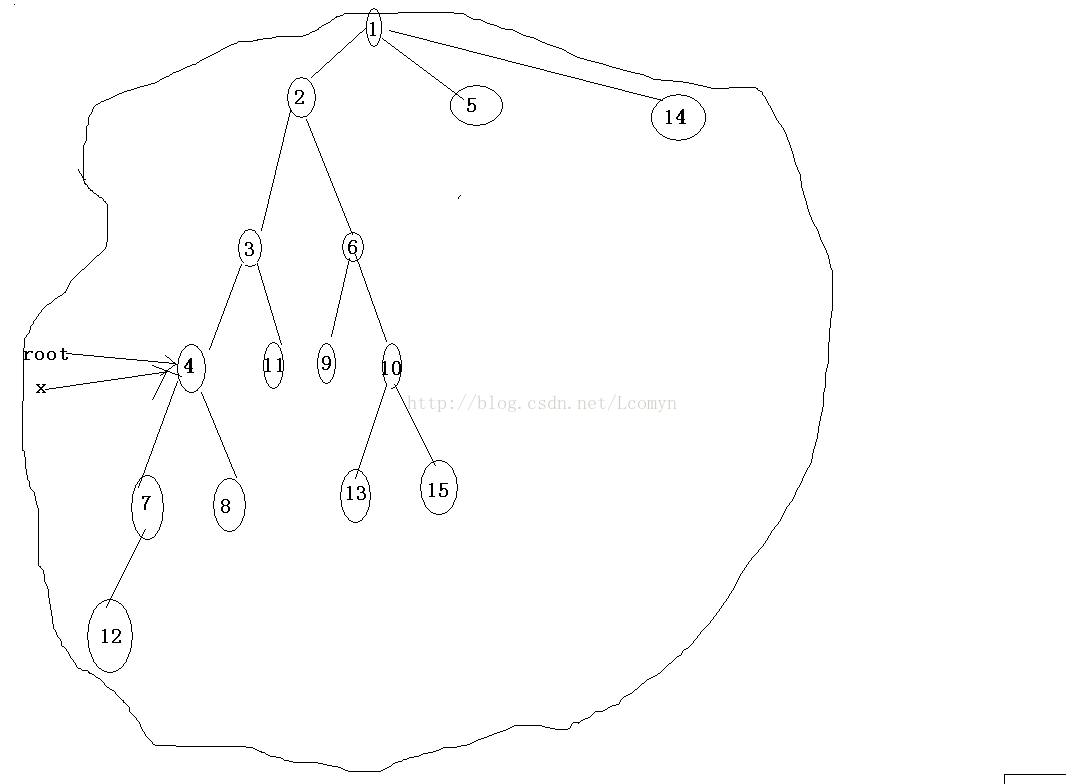
第二种情况:$lca(x,root) != x$
这种情况也简单,直接查询$x$子树中的最小值即可
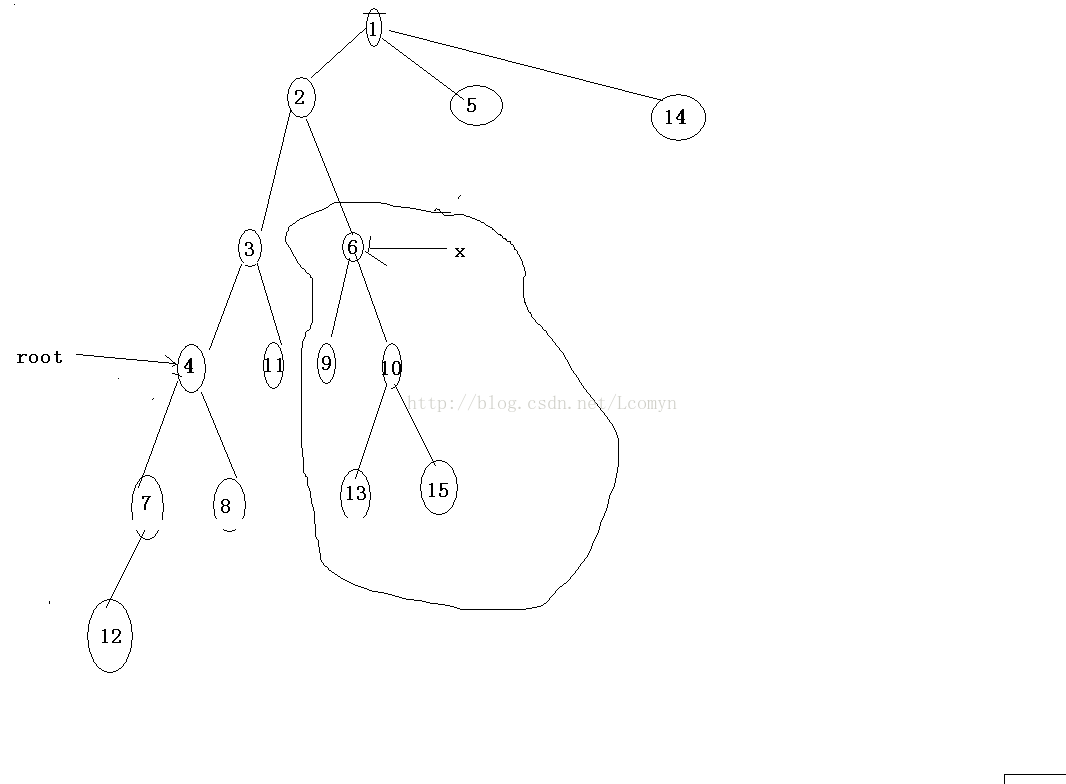
第三种情况:$lca(x,root) = x$
这种情况稍微复杂一些
我们需要找到$root$往上走,离$x$最近的点。
很显然,这个点以上的部分,就是我们要查询的区间
那么我们查询这个点的子树对应区间的补集即可

#include<cstdio> #include<vector> #include<algorithm> using namespace std; const int MAXN = 1e5 + 10, B = 20, INF = 2147483646; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, root = 1; int a[MAXN], b[MAXN]; vector<int> v[MAXN]; int fa[MAXN], top[MAXN], jump[MAXN][21], deep[MAXN], siz[MAXN], l[MAXN], r[MAXN], tot = 0, cnt, son[MAXN], ID[MAXN]; void dfs1(int x, int _fa) { fa[x] = _fa; siz[x] = 1; l[x] = ++cnt; jump[x][0] = fa[x]; for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; if(deep[to]) continue; deep[to] = deep[x] + 1; dfs1(to, x); siz[x] += siz[to]; if(siz[to] > siz[son[x]]) son[x] = to; } r[x] = cnt; } void dfs2(int x, int topf) { top[x] = topf; ID[x] = ++tot; a[tot] = b[x]; l[x] = tot; if(!son[x]) {r[x] = tot; return ;} dfs2(son[x], topf); for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; if(top[to]) continue; dfs2(to, to); } r[x] = tot; } void Pre() { for(int i = 1; i <= B; i++) for(int j = 1; j <= N; j++) jump[j][i] = jump[jump[j][i - 1]][i - 1]; } #define ls k << 1 #define rs k << 1 | 1 struct Node { int l, r, mi, si, tag; }T[MAXN * 4]; void update(int k) {T[k].mi = min(T[ls].mi, T[rs].mi);} void ps(int k, int val) {T[k].mi = val; T[k].tag = val; return ;} void pushdown(int k) { if(!T[k].tag) return; ps(ls, T[k].tag); ps(rs, T[k].tag); T[k].tag = 0; } void Build(int k, int ll, int rr) { T[k].l = ll; T[k].r = rr; T[k].si = r - l + 1; if(ll == rr) {T[k].mi = a[ll]; return ;} int mid = ll + rr >> 1; Build(ls, ll, mid); Build(rs, mid + 1, rr); update(k); } void IntervalMem(int k, int ll, int rr, int val) { if(ll <= T[k].l && T[k].r <= rr) { T[k].mi = T[k].tag = val; return; } pushdown(k); int mid = T[k].l + T[k].r >> 1; if(ll <= mid) IntervalMem(ls, ll, rr, val); if(rr > mid) IntervalMem(rs, ll, rr, val); update(k); } void TreeChange(int x, int y, int val) { while(top[x] != top[y]) { if(deep[top[x]] < deep[top[y]]) swap(x, y); IntervalMem(1, ID[top[x]], ID[x], val); x = fa[top[x]]; } if(deep[x] < deep[y]) swap(x, y); IntervalMem(1, ID[y], ID[x], val); } int IntervalMin(int k, int ll, int rr) { int ans = INF; if(ll <= T[k].l && T[k].r <= rr) return T[k].mi; pushdown(k); int mid = (T[k].l + T[k].r) >> 1; if(ll <= mid) ans = min(ans, IntervalMin(ls, ll, rr)); if(rr > mid) ans = min(ans, IntervalMin(rs, ll, rr)); return ans; } int LCA(int x, int y) { while(top[x] != top[y]) { if(deep[top[x]] < deep[top[y]]) swap(x, y); x = fa[top[x]]; } if(deep[x] < deep[y]) swap(x, y); return y; } int Find(int rt, int x) { for(int i = B; i >= 0; i--) while(deep[jump[rt][i]] > deep[x]) rt = jump[rt][i]; return rt; } int Query(int x) { if(x == root) return T[1].mi; int lca = LCA(x, root); if(lca != x) return IntervalMin(1, l[x], r[x]); int v = Find(root, x), ans = INF; if(l[v] > 1) ans = min(ans, IntervalMin(1, 1, l[v] - 1));//tag if(r[v] < N) ans = min(ans, IntervalMin(1, r[v] + 1, tot)); return ans; } int main() { N = read(); M = read(); for(int i = 1; i <= N - 1; i++) { int x = read(), y = read(); v[x].push_back(y); v[y].push_back(x); } for(int i = 1; i <= N; i++) b[i] = read(); root = read(); deep[1] = 1; dfs1(1, 0); dfs2(1, 1); Pre(); Build(1, 1, tot); while(M--) { int opt = read(); if(opt == 1) root = read(); else if(opt == 2){ int x1 = read(), x2 = read(), v = read(); TreeChange(x1, x2, v); } else { int x = read(); printf("%d ", Query(x)); } } return 0; } /* 3 7 1 2 1 3 1 2 3 1 3 1 2 1 1 6 3 1 2 2 2 5 3 1 2 3 3 4 3 1 */