POJ2409 Let it Bead(Polya定理)

Let it Bead

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 6443		Accepted: 4315

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced. 

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

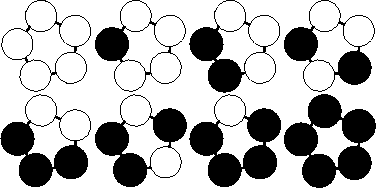For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0

Sample Output

1
2
3
5
8
13
21

Source

感觉这玩意儿认真的好神奇啊qwq。

为什么网上都是直接说循环节的大小但是不做说明qwq、、

算了还是背结论吧

若是直接旋转，那么有$n$中置换，第$i$种循环节数为$gcd(n, i)$

如果是对称

对于奇数来说，可以固定一个点，让其他点交换。共有$n$个点，每种循环节为$frac{n + 1}{2}$

对于偶数来说，有两种对称方式，

一种是以中线为中心，两边对称，共有$N / 2$种方式，每种循环节为$frac{n + 2}{2}$

另一种是两个点的连线为中心，两边对称，共有$N/ 2$种方式，每种循环节为$frac{n}{2}$

然后直接上polya定理就行了

POJ的评测机也是没谁了

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<map>
#define LL long long  
const int MAXN = 1e5 + 10;
using namespace std;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int C, N;
int fastpow(int a, int p) {
    int base = 1;
    while(p) {
        if(p & 1) base = base * a;
        a = a * a; p >>= 1;
    }
    return base;
}
main() {
    while(scanf("%d %d", &C, &N)) {
        if(C == 0 && N == 0) break;
        int ans = 0;
        for(int i = 1; i <= N; i++) ans += fastpow(C, __gcd(i, N));
        if(N & 1) ans = ans + N * fastpow(C, (N + 1) / 2);
        else ans = ans + N / 2  * (fastpow(C, (N + 2) / 2) + fastpow(C, N / 2));
        printf("%d
", ans / 2 / N);
    }
}