本博客仅用来记录重要概念。
线性代数学习请移步https://www.bilibili.com/video/av6731067
不得不说,这位up主讲的是真心好,尤其是点积叉积那一部分,直接刷新世界观QWQ。
基
空间内的一组基指的是:张成该空间的一个线性无关向量的集合

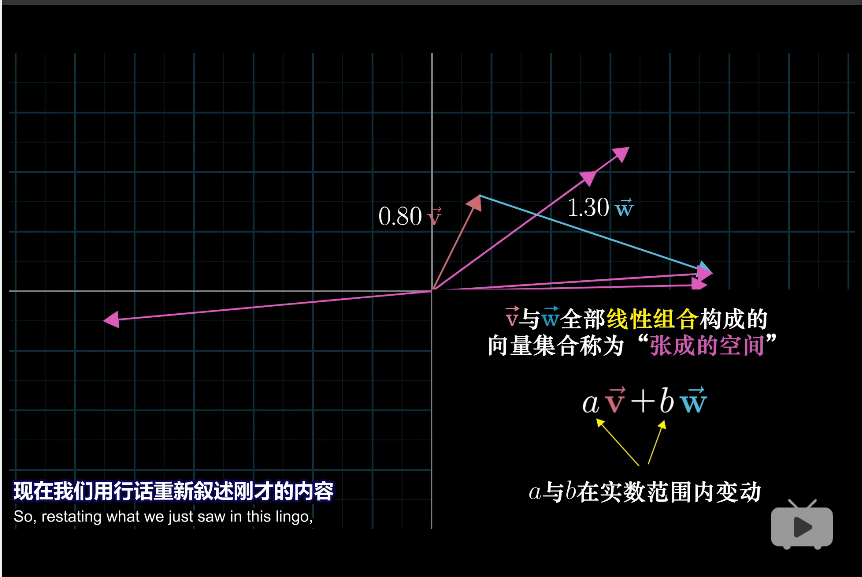
张成
所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间
张成在这里应该是动词。
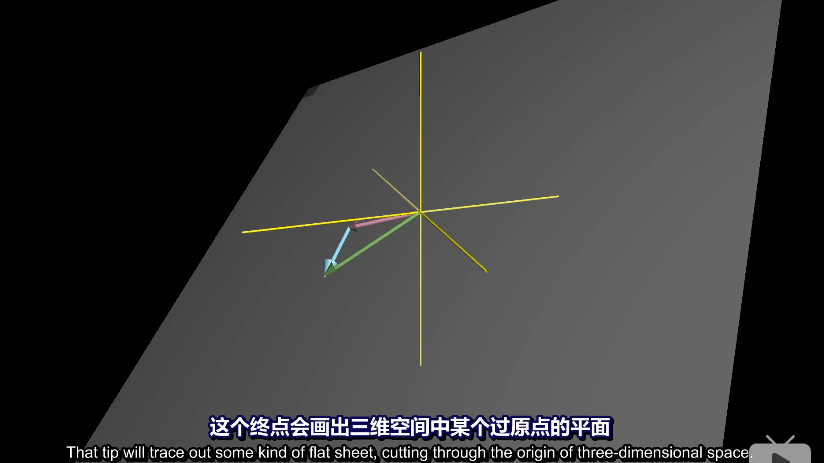
在三维空间中,两个向量张成出的空间应该是某个过原点的平面
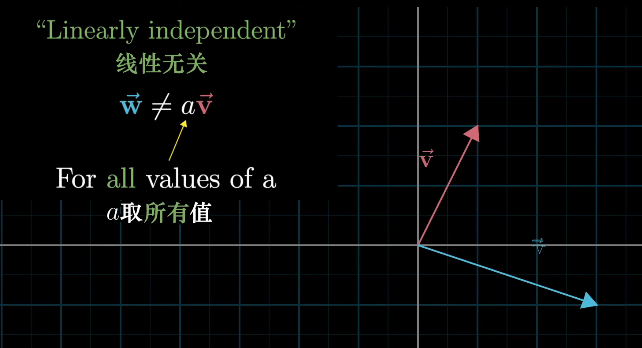
线性相关
一组向量中至少有一个是多余的,没有对张成空间做出任何贡献
你有多个向量, 并且可以移除其中的一个而不减小张成的空间
这种情况发生时,我们称他们是“线性相关”的

如果所有的向量都给张成的空间增加了新的维度,他们就被称为“线性无关”
矩阵
这介绍怎么这么鬼畜。。


对空间的一种特定变换
线性变换
接收一个向量,并输出一个向量的变换
线性的直观含义:
1.直线在变换后仍然为直线,不能有所弯曲
2.原点必须保持固定(如果原点不固定,它可能为“仿射变换”)
注意:线性变换“保持网格线平行且等距分布”—》如果变换前的向量是$i$和$j$的线性组合,那么变换后也是$i$和$j$的线性组合


矩阵乘法
复合矩阵

乘积需要从右往左计算
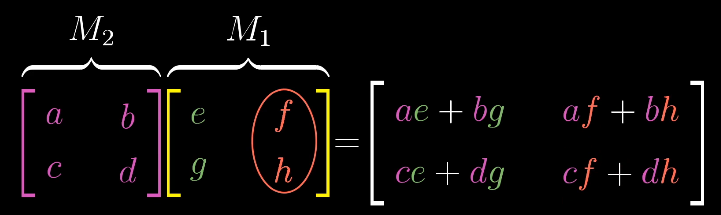
我对矩阵乘法的理解:
首先把$M_1$的$[e,g]$看成一个向量,$[f,h]$看成一个向量
左乘$M_2$实际是两个向量分别与$M_2$相乘
$M_2$可以看做将基底进行变换的矩阵
根据线性变换的性质,
$[e,g]$所代表的向量为$ei + gj$,此时$i$变为$(a,c)$,$j$变为$(b, d)$
然后带入相乘就得到了最终答案
矩阵乘法的性质
不满足交换律
对于变换$A,B$,先应用$A$再应用$b$
和线应用$B$,再应用$A$,得到的结果是不同的


满足结合律
$(AB)C$相当于先应用$C$变换,再应用$B$、$A$变换
$A(BC)$相当于先应用$C$、$B$变换,再应用$A$变换,
他们的运算顺序是相同的
三维空间内的线性变换
本质与二维是相同的
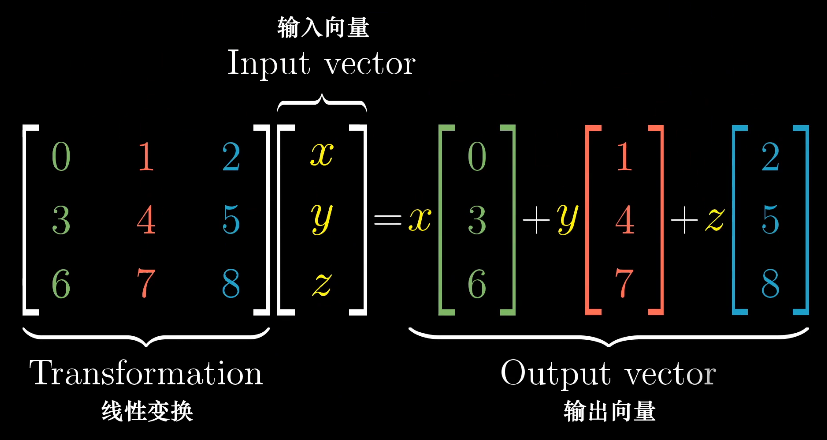
行列式
二维空间
线性变换改变面积的比例被称为这个变换的行列式

当空间定向改变的情况发生时行列式为负
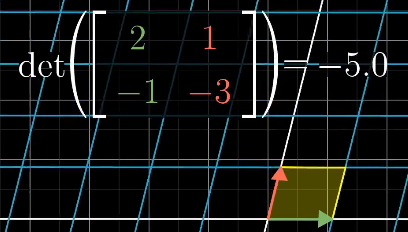
三维空间
三维空间下行列式的值为平行六面体的体积
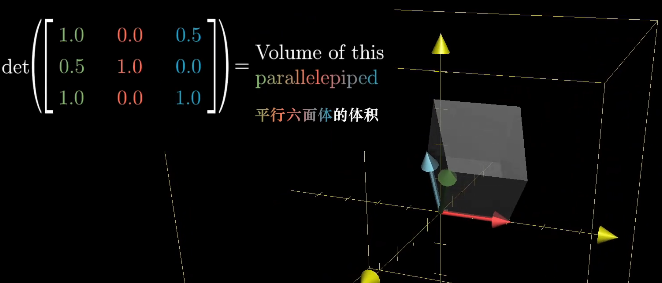
判断正负的方法:
右手定则:让食指指向$i$,中指指向$j$,拇指指向$k$,如果变换之后仍然能这么做,则为正;若只能用食指这么做,则为负
行列式的计算
二维

证明:
三维:
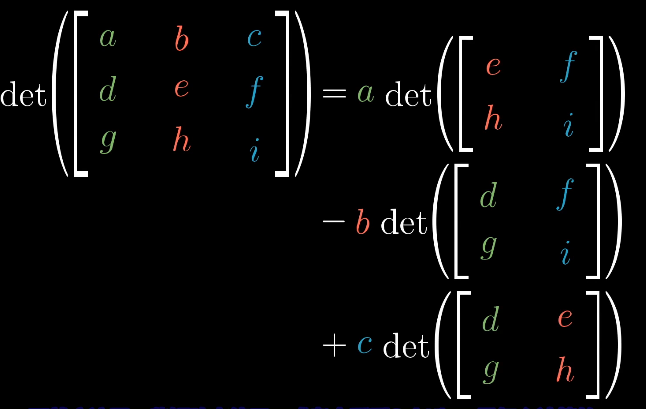
性质
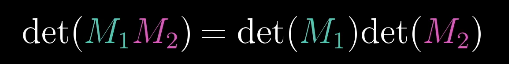
逆矩阵

矩阵的秩
秩:变换后空间的维数/列空间的维数

满秩:秩与列数相同
列空间
直线/平面/三维空间等,所有可能的变换结果的集合,被称为矩阵的“列空间”

零空间
零空间:变换后落在原点的向量的集合
点积
定义:
代数:对于两个维度相同的矩阵,其点积为将相应坐标配对,求出每一对坐标的乘积再相加
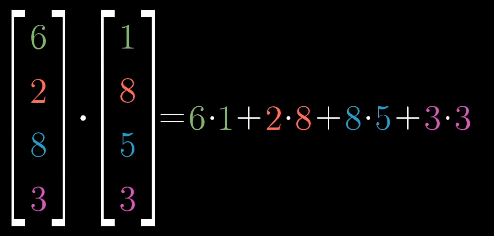
几何:两个向量的点积为一个向量在另一个向量上正交投影的长度乘以另一个向量的长度(好绕。。)
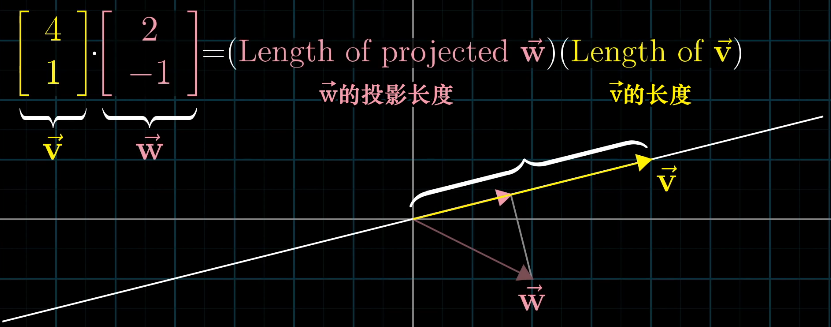
若两向量反向,则乘积为负
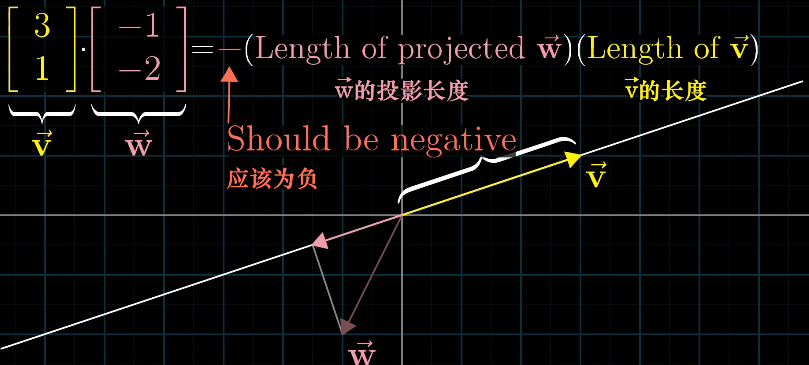
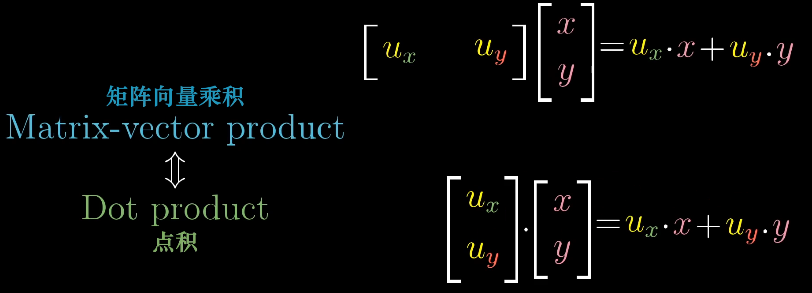
两者的关系:
这一部分听傻了,感觉都是神仙推导。太强了orz
叉积
定义
视频中并没有明确的给出叉积的定义
大概就是算出两个向量的行列式来构成第三个向量
正负
对于$i imes j$,若$i$在$j$右侧,则叉积为正,否则叉积为负

计算
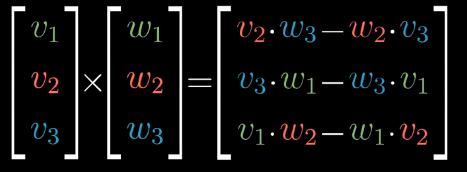
基变换
感觉前面讲过。。
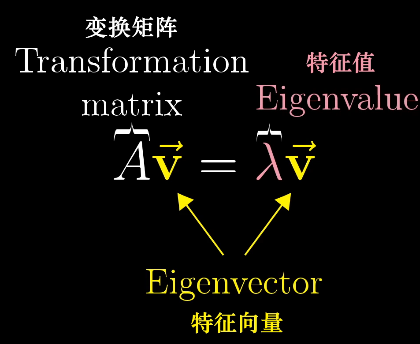
特征向量与特征值
定义
特征向量
在基向量变换后张成出的空间与基向量不变时张成出的空间相同的向量?
特征值
特征向量在变换后被缩放/拉伸的比例