前言
网络最大流是网络流中最基础也是最重要的部分,后边的许多模型也都是由最大流问题引申而来的
最大流
在研究这个问题之前,让我们先来学习一下前置知识
可行流
设$f(u,v)$表示边$(u,v)$的当前容量上限
设$c(u,v)$表示边$(u,v)$的最大容量上限
如果网络流图中的流量满足
- 源点$S$:流出量$=$流量总量
- 汇点$T$:流入量$=$流量总量
- 任意边$(u,v)$:$0<=f(u,v)<=c(u,v)$
则称该流为一个可行流
增广
增广:即增加一条路径上的流量
增加一条路径的流量,即减少这条路径的当前流量上限,即$f(u,v)$的值
增广是我们求解最大流的基础
最大流
定义:在所有可行流中流量最大的流
那么我们如何求解这个东西呢?
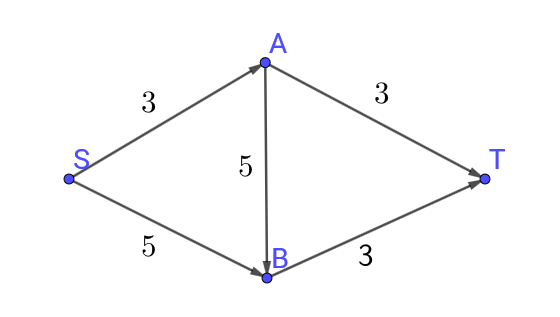
很显然的一种思路就是找到整个网络中的容量上限最小的边
增广(就是加流量)这条路径,不断的重复
暂且不说这么做时间复杂度如何
我们先考虑一下它的正确性。
这么做貌似很有道理,
但是!
以上图为例,如只是无脑增广的话,很可能对SABT这条边进行增广,而增广完这条边后,就再也没有可以增广的路径了,求出的最大流为$3$,下图为增广后的网络流图
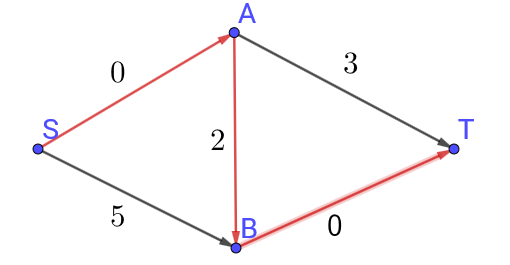
很显然,这么做是错的,因为我们可以分别增广$SAT$,$SBT$这两条路径,得到的流量为$6$
那怎么解决这个问题呢?
我们需要引入一个非常重要的概念——反向边
例如,对于$SA$这条容量为$3$的边,我们可以认为存在一条容量为$0$的边$AS$与之对应,对于$SA$进行增广,即减小它的容量上限,相当于增大$AS$的容量上限
也就是说,我们允许从$SA$流出的流量倒流回去,给它一个悔改的机会
这样,对于上图而言,我们可以借助反向边来更改自己的错误操作,建立反向边后的图如下图所示
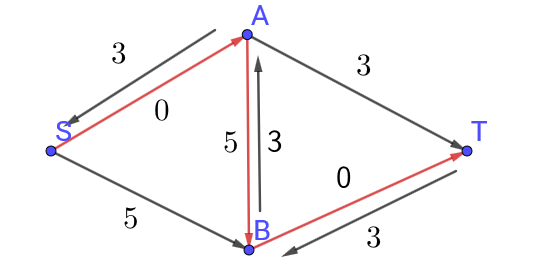
这样我们便又有了一条新的增广路$SBAT$,对这条路径进行增广后我们便可以得到网络最大流为$5$
考虑一下,为什么这样是对的?
原因很简单,造成我们刚开始做出错误决策的边为$AB$,最大流本不应经过这里,但是我们却无脑的经过了这里
因为反向边$BA$的存在,我们又把从$A$流向$B$的流量给退了回去。这就相当于没有经过$AB$这条边
(本节以下内容读者可以直接略过,属于本蒟蒻瞎扯,可能把读者带到沟里面,目前已有一人受害)
反向弧到这里本就应该结束了,但是本蒟蒻在学习的过程中一直有个问题不明白
为什么加反向弧是对的?
如果不考虑反向弧,我们选择的路径为$SAT$,$SBT$,但是加了反向弧之后我们的路径貌似不是这么选的啊。。
尤其是$AT$这条边的流量,本应该是从$SA$流过来,但实际是从$SB$流过来。
这样为什么是对的呢?
这个问题我思考了很长时间,最终得出了一个很不靠谱的结论
因为经过$AB$这条边的流量为$SA,AB,BT$的最小值,然后xjb分情况讨论一下,%……&*()()*&……%¥)(大概要分个一二十种情况吧,然后发现都是对的,其实就是各边之间的流量等效替代问题。。。)
看到这儿的同学,恭喜你们被带到坑里啦O(∩_∩)O哈哈~
实现
我目前见过的最大流算法有以下几种
- EK(最简单,比较慢)
- Dinic(最常见,性能良好)
- ISAP/SAP(也比较常见,性能很好)
- 最高标号预流推进(HLPP) (暂时还没学。。)
- 前置重贴标签(什么鬼。。。)
- 推送重贴标签(WTF......)
对于这些算法,博主给大家的建议是:
- 理解第一种方法,并用代码实现一次
- 熟练掌握第二种算法,深刻的理解其内涵,并能做到超级熟练的运用(起码5min之内要敲出来&&没有错误)
- 理解第三种算法,并至少运用一次。(因为第三种算法跑的比较快,所以可以用来抢排行榜$rank1$)
- 第四五六中算法建议大家理解其内涵,代码实现就无所谓了,因为基本用不到,不过学会了可以用来装13:joy:
另外,在书上看到过据说可以使用动态树优化最大流算法,但是把百度翻遍了也没找到代码。。。
如果您会的话欢迎教一下本蒟蒻,感激不尽
由于想讲的详细一些,所以想了一下把每个算法分开讲吧,我会尽快更新哒:grinning:
(最近这几天可能不太好办了,因为博主在外面学(bei)习(nue),只有晚上才能更博客)